
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,射线
,射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆
交半圆![]() 于点
于点![]() ,连接
,连接![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过点
.过点![]() 作半圆的切线
作半圆的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
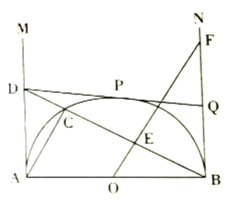
科目:初中数学 来源: 题型:
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
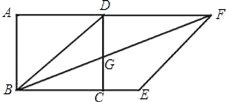
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
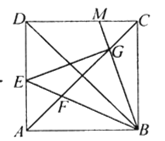
【题目】如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A,D不重合),![]() ,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
(1)求DE:CG的值;
(2)设![]() ,
,![]() ,
,
①求y关于x的函数表达式及x的取值范围.
②当图中点E,M关于对角线BD成轴对称时,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
|
|
| |
笔试 |
|
|
|
口试 |
|
|
|
形象 |
|
|
|
平均分 |
|
|
|
(1)①![]() ;
;
②在表格中的![]() 个数的中位数是 ,众数是
个数的中位数是 ,众数是
(2)经学校研究决定,在![]() 两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分
两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分![]() 进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?
进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以每秒
上一动点,以每秒![]() 个单位长度的速度从
个单位长度的速度从![]() 出发向
出发向![]() 运动,以
运动,以![]() ,
,![]() 为边作矩形
为边作矩形![]() ,直线
,直线![]() 与直
与直![]() 、
、![]() 的交点分别为
的交点分别为![]() ,
,![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() .
.

(1)![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
(2)当四边形![]() 是正方形时,求
是正方形时,求![]() 的长.
的长.
(3)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
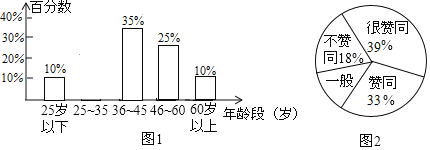
【题目】某城市响应“绿水青山就是金山银山”的号召,准备在全市宣传开展“垃圾分类”活动,先对随机抽取的![]() 名公民的年龄段分布情况和对“垃圾分类”所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
名公民的年龄段分布情况和对“垃圾分类”所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)补全条形图;
(2)扇形图中态度为“一般”所对应的扇形的圆心角的度数是 ;
(3)这次随机调查中,年龄段是“![]() 岁一下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ;
岁一下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,这个城市总人口大约![]() 万人,则对开展“垃圾分类”持“支持”态度的估计有多少万人?
万人,则对开展“垃圾分类”持“支持”态度的估计有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“掷一次骰子,向上一面的点数是![]() ”是必然事件
”是必然事件
B.掷一枚硬币正面朝上的概率是![]() 表示每抛硬币
表示每抛硬币![]() 次就有
次就有![]() 次正面朝上
次正面朝上
C.计算甲组和乙组数据,得知![]() ,
,![]() ,
,![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
D.一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的众数和中位数都是
的众数和中位数都是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线交AD于E,交BC于F,连接BE 、DF.

(1)判断四边形BEDF的形状,并说明理由;
(2)若AB=8,AD=16,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com