练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】三位女同学竞选学校即将组织的“中国梦，我的梦”文艺演出女主持人，它们的笔试成绩和口试成绩、形象得分，分别如下：

    笔试

    口试

    形象

    平均分

    （1）① ；

    ②在表格中的个数的中位数是 ，众数是

    （2）经学校研究决定，在两位同学中选一位．评比方法：按笔试成绩：口试成绩：形象得分进行计算，得分最高的同学为本次文艺演出的女主持人．请你算一算哪位同学最后被选为本次文艺演出的女主持人？

    【答案】（1）①；②；；（2）最后B同学被选为本次文艺汇演的女主持人．

    【解析】

    （1）①根据平均数的定义直接计算即可得到n的值；②将这12个数按从小到大的顺序排列，取中间两个数的平均数即为中位数，出现次数最多的数即为众数；

    （2）根据加权平均数的计算方法即可求得哪位的成绩高从而得到答案．

    （1）①

    ②将这12个数排列如下：88，89，90，90，91，91，92，92，92，92，93，96，

    则中间两个数是 91和92，故中位数为；

    出现次数最多的是92，故众数是92；

    （2）同学最后得分：

    同学最后得分：

    又

    最后B同学被选为本次文艺汇演的女主持人．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

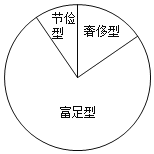
    【题目】某校为了解学生零用钱支出情况，从七、八、九年级800名学生中随机抽取部分学生，对他们今年5月份的零用钱支出情况进行调查统计，并绘制成如下统计图表：

    组别

    零用钱支出x（单位：元）

    频数（人数）

    频率

    节俭型

    一

    x＜20

    m

    0.05

    二

    20≤x＜30

    4

    a

    富足型

    三

    30≤x＜40

    n

    0.45

    四

    40≤x＜50

    12

    b

    奢侈型

    五

    x≥50

    4

    c

    合计

    1

    （1）表中a+b+c＝　 　；m＝　 　；本次调查共随机抽取了　 　名同学；

    （2）在扇形统计图中，“富足型”对应的扇形的圆心角的度数是　 　；

    （3）估计今年5月份全校零花钱支出在30≤x＜40范围内的学生人数；

    （4）在抽样的“奢侈型”学生中，有2名女生和2名男生．学校团委计划从中随机抽取2名同学参加“绿苗理财计划”活动，请运用树状图或者列表说明恰好抽到一男一女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现

    如图①，是等腰直角三角形，四边形是正方形，点与点重合，则线段与之间的数量关系和位置关系分别是 ．

    （2）深入探究

    如图②，是等腰直角三角形，四边形是正方形，点在直线上，对角线所在的直线交直线于点，则线段之间有什么数量关系？请仅就图②给出证明．

    （3）拓展思维

    如图②，若点在直线上，且线段，当时，直接写出此时正方形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

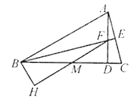
    【题目】如图，△ABC中，，于点D，于点E，交AD于点F，点M是BC的中点，连接FM并延长交AB的垂线BH于点H．下列说法中错误的是（ ）

    A.若，则

    B.若，则

    C.若（点M与点D重合），则

    D.若（点B与点D重合），则

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种植户计划将一片荒山改良后种植沃柑，经市场调查得知，当种植沃柑的面积x不超过15亩时，每亩可获得利润y=1900元；超过15亩时，每亩获得利润y（元）与种植面积x（亩）之间的函数关系:y=kx+b，并且当x=20时，y=1800；当x=25时，y=1700．

    （1）请求出y与x的函数关系式，并写出自变量的取值范围；

    （2）设种植户种植x亩沃柑所获得的总利润为w元，由于受条件限制，种植沃柑面积x不超过50亩，求该种植户种植多少亩获得的总利润最大，并求总利润w（元）的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

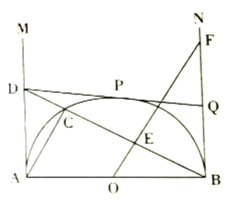
    【题目】如图，是半圆的直径，，射线为半圆的切线．在上取一点，连接交半圆于点，连接．过点作，垂足为点，与相交于点．过点作半圆的切线，切点为，与相交于点．

    （1）求证：；

    （2）当与的面积相等时，求的长；

    （3）求证：当在上移动时（点除外），点始终是线段的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】疫情期间，口罩供不应求．某口罩企业为指导生产，在二月份期间对甲乙丙丁四条生产线日产量进行调研，根据调研数据，绘制出如下两幅不完整的统计图．观察统计图，请解答以下问题：

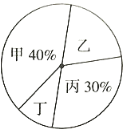
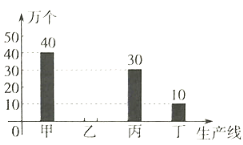
    （1）求二月份该企业口罩单日产量（二月份计天）．

    （2）求乙条生产线单日产量是多少，并补全频数分布直方图．

    （3）为满足市场需求，该公司改进生产技术，使得口罩产量在二月的基础上逐月提高，已知月份口罩产量为万只，若三月份和四月份口罩月产量平均增长率相同，求每月的平均增长率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某水产养殖户开发一个三角形状的养殖区域，A、B、C三点的位置如图所示．已知∠CAB=105°，∠B=45°，AB=100米．（参考数据：≈1．41，≈1．73，sin20°≈0．34，cos20°≈0．94，tan20°≈0．36，结果保留整数）

    （1）求养殖区域△ABC的面积；

    （2）养殖户计划在边BC上选一点D，修建垂钓栈道AD，测得∠CAD=40°，求垂钓栈道AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

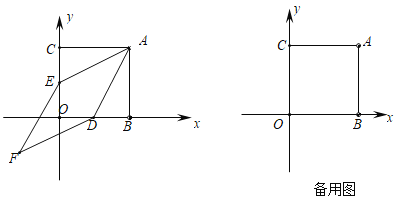
    【题目】如图，在平面直角坐标系中，正方形ABOC的两直角边分别在坐标轴的正半轴上，分别过OB，OC的中点D，E作AE，AD的平行线，相交于点F， 已知OB=8．

    （1）求证：四边形AEFD为菱形．

    （2）求四边形AEFD的面积．

    （3）若点P在x轴正半轴上(异于点D)，点Q在y轴上，平面内是否存在点G，使得以点A，P， Q，G为顶点的四边形与四边形AEFD相似？若存在，求点P的坐标；若不存在，试说明理由．

    查看答案和解析>>

    同步练习册答案