
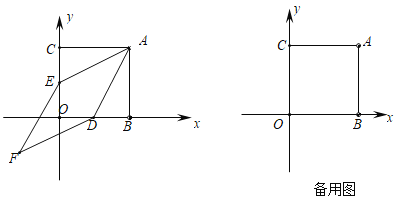
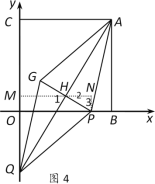
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮABOCЕФСНжБНЧБпЗжБ№дкзјБъжсЕФе§АыжсЩЯЃЌЗжБ№Й§OBЃЌOCЕФжаЕуDЃЌEзїAEЃЌADЕФЦНааЯпЃЌЯрНЛгкЕуFЃЌ вбжЊOB=8ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAEFDЮЊСтаЮЃЎ
ЃЈ2ЃЉЧѓЫФБпаЮAEFDЕФУцЛ§ЃЎ
ЃЈ3ЃЉШєЕуPдкxжсе§АыжсЩЯ(вьгкЕуD)ЃЌЕуQдкyжсЩЯЃЌЦНУцФкЪЧЗёДцдкЕуGЃЌЪЙЕУвдЕуAЃЌPЃЌ QЃЌGЮЊЖЅЕуЕФЫФБпаЮгыЫФБпаЮAEFDЯрЫЦЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ48ЃЛЃЈ3ЃЉЕуPЕФзјБъЮЊ(12ЃЌ0)ЃЌ(24ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(
ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(16ЃЌ0)
ЃЌ0)ЃЌ(16ЃЌ0)
ЁОНтЮіЁП
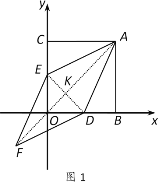
ЃЈ1ЃЉНсКЯе§ЗНаЮаджЪЧѓЕУЁїACEЁеЁїABDЃЌДгЖјЕУЕНAE=ADЃЌИљОнСкБпЯрЕШЕФЦНааЫФБпаЮЪЧСтаЮжЄУїМДПЩЃЎ
ЃЈ2ЃЉСЌНгDEЃЌЧѓГіЁїADEЕФУцЛ§МДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЪзЯШжЄУїAK=3DKЃЌЂйЕБAPЮЊСтаЮЕФвЛБпЃЌЕуQдкxжсЕФЩЯЗНЃЌгаЭМ2ЃЌЭМ3СНжжЧщаЮЃЎЂкЕБAPЮЊСтаЮЕФБпЃЌЕуQдкxжсЕФЯТЗНЪБЃЌгаЭМ4ЃЌЭМ5СНжжЧщаЮЃЎЂлШчЭМ6жаЃЌЕБAPЮЊСтаЮЕФЖдНЧЯпЪБЃЌгаЭМ6вЛжжЧщаЮЃЎЗжБ№РћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁпDFЁЮAEЃЌEFЁЮADЃЌ
ЁрЫФБпаЮAEFDЪЧЦНааЫФБпаЮ.
ЁпЫФБпаЮABOCЪЧе§ЗНаЮЃЌ
ЁрOBЃНOCЃНABЃНACЃЌЁЯACEЃНЁЯABDЃН90Ёу.
ЁпЕуDЃЌEЪЧOBЃЌOCЕФжаЕуЃЌ
ЁрCEЃНBDЃЌ
ЁрЁїACEЁеЁїABD(SAS)ЃЌ
ЁрAEЃНADЃЌ
Ёр![]() ЪЧСтаЮ
ЪЧСтаЮ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНсDE
ЁпSЁїABDЃН![]() ABЁЄBDЃН
ABЁЄBDЃН![]() ЃЌ SЁїODEЃН
ЃЌ SЁїODEЃН![]() ODЁЄOEЃН
ODЁЄOEЃН![]() ЃЌ
ЃЌ
ЁрSЁїAEDЃНSе§ЗНаЮABOCЃ2 SЁїABDЃ SЁїODEЃН64Ѓ2![]() Ѓ8ЃН24ЃЌ
Ѓ8ЃН24ЃЌ
ЁрSСтаЮAEFDЃН2SЁїAEDЃН48
ЃЈ3ЃЉгЩЭМ1ЃЌСЌНсAFгыDEЯрНЛгкЕуKЃЌвзЕУЁїADKЕФСНжБНЧБпжЎБШЮЊ1:3
1ЃЉЕБAPЮЊСтаЮвЛБпЪБЃЌЕуQдкxжсЩЯЗНЃЌгаЭМ2ЁЂЭМ3СНжжЧщПіЃК
ШчЭМ2ЃЌAGгыPQНЛгкЕуHЃЌ
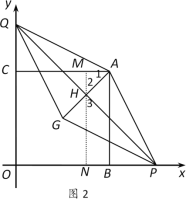
ЁпСтаЮPAQGЁзСтаЮADFEЃЌ
ЁрЁїAPHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHNЁЭxжсгкЕуNЃЌНЛACгкЕуMЃЌЩшAM=t
ЁпHNЁЮOQЃЌЕуHЪЧPQЕФжаЕуЃЌ
ЁрЕуNЪЧOPжаЕуЃЌ
ЁрHNЪЧЁїOPQЕФжаЮЛЯпЃЌ
ЁрONЃНPNЃН8Ѓt
гжЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯPNHЃНЁЯAMHЃН90ЁуЃЌ
ЁрЁїHMAЁзЁїPNHЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрHNЃН3AMЃН3tЃЌ
ЁрMHЃНMNЃNHЃН8Ѓ3t.
ЁпPNЃН3MHЃЌ
Ёр8Ѓt =3(8Ѓ3t)ЃЌНтЕУtЃН2
ЁрOPЃН2ONЃН2(8Ѓt)ЃН12
ЁрЕуPЕФзјБъЮЊ(12ЃЌ0)
ШчЭМ3ЃЌЁїAPHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHIЁЭyжсгкЕуIЃЌЙ§ЕуPзїPNЁЭxжсНЛIHгкЕуNЃЌбгГЄBAНЛINгкЕуM
ЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯAMHЃНЁЯPNHЃЌ
ЁрЁїAMHЁзЁїHNPЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌЩшMHЃНtЃЌ
ЃЌЩшMHЃНtЃЌ
ЁрPNЃН3MHЃН3tЃЌ
ЁрAMЃНBMЃABЃН3tЃ8ЃЌ
ЁрHNЃН3AMЃН3(3tЃ8) ЃН9tЃ24
гжЁпHIЪЧЁїOPQЕФжаЮЛЯпЃЌ
ЁрOPЃН2IHЃЌ
ЁрHIЃНHNЃЌ
Ёр8ЃЋtЃН9tЃ24ЃЌНтЕУ tЃН4
ЁрOPЃН2HIЃН2(8ЃЋt)ЃН24ЃЌ
ЁрЕуPЕФзјБъЮЊ(24ЃЌ0)
2ЃЉЕБAPЮЊСтаЮвЛБпЪБЃЌЕуQдкxжсЯТЗНЃЌгаЭМ4ЁЂЭМ5СНжжЧщПіЃК
ШчЭМ4ЃЌЁїPQHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHMЁЭyжсгкЕуMЃЌЙ§ЕуPзїPNЁЭHMгкЕуN
ЁпMHЪЧЁїQACЕФжаЮЛЯпЃЌ
ЁрHMЃН![]() ЃН4
ЃН4
гжЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯHMQЃНЁЯNЃЌ
ЁрЁїHPNЁзЁїQHMЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌдђPNЃН
ЃЌдђPNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрOMЃН![]()
ЩшHNЃНtЃЌдђMQЃН3t
ЁпMQЃНMCЃЌ
Ёр3tЃН8Ѓ![]() ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]()
ЁрOPЃНMNЃН4ЃЋtЃН![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ(![]() ЃЌ0)
ЃЌ0)
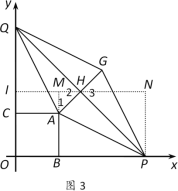
ШчЭМ5ЃЌЁїPQHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHMЁЭxжсгкЕуMЃЌНЛACгкЕуIЃЌЙ§ЕуQзїNQЁЭHMгкЕуN

ЁпIHЪЧЁїACQЕФжаЮЛЯпЃЌ
ЁрCQЃН2HIЃЌNQЃНCIЃН4
ЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯPMHЃНЁЯQNHЃЌ
ЁрЁїPMHЁзЁїHNQЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌдђMHЃН
ЃЌдђMHЃН![]() NQЃН
NQЃН![]()
ЩшPMЃНtЃЌдђHNЃН3tЃЌ
ЁпHNЃНHIЃЌ
Ёр3tЃН8+![]() ЃЌНтЕУ tЃН
ЃЌНтЕУ tЃН![]()
ЁрOPЃНOMЃPMЃНQNЃPMЃН4ЃtЃН![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ(![]() ЃЌ0)
ЃЌ0)
3ЃЉЕБAPЮЊСтаЮЖдНЧЯпЪБЃЌгаЭМ6вЛжжЧщПіЃК
ШчЭМ6ЃЌЁїPQHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHMЁЭyжсгкЕуMЃЌНЛABгкЕуIЃЌЙ§ЕуPзїPNЁЭHMгкЕуN
ЁпHIЁЮxжсЃЌЕуHЮЊAPЕФжаЕуЃЌ
ЁрAIЃНIBЃН4ЃЌ
ЁрPNЃН4
ЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯPNHЃНЁЯQMHЃН90ЁуЃЌ
ЁрЁїPNHЁзЁїHMQЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌдђMHЃН3PNЃН12ЃЌHIЃНMHЃMIЃН4
ЃЌдђMHЃН3PNЃН12ЃЌHIЃНMHЃMIЃН4
ЁпHIЪЧЁїABPЕФжаЮЛЯпЃЌ
ЁрBPЃН2HIЃН8ЃЌМДOPЃН16ЃЌ
ЁрЕуPЕФзјБъЮЊ(16ЃЌ0)
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊ(12ЃЌ0)ЃЌ(24ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(
ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(16ЃЌ0)ЃЎ
ЃЌ0)ЃЌ(16ЃЌ0)ЃЎ


 КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ
КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
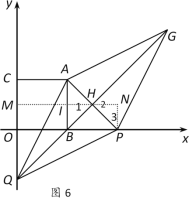
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌAB=5ЃЌAC=6ЃЌACЕФЦНааЯпDEНЛBCЕФбгГЄЯпгкЕуEЃЌдђЫФБпаЮACEDЕФУцЛ§ЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуOЮЊЁїABCЕФСНЬѕНЧЦНЗжЯпЕФНЛЕуЃЌЙ§ЕуOзїODЁЭBCЃЌДЙзуЮЊDЃЌЧвODЃН4ЃЎШєЁїABCЕФУцЛ§ЪЧ34ЃЌдђЁїABCЕФжмГЄЮЊЃЈЁЁЁЁЃЉ

A.8.5B.15C.17D.34
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпCЃКyЃН![]() x[aЃЈxЉ1ЃЉ+x+1]ЃЈaЮЊШЮвтЪЕЪ§ЃЉЃЎ
x[aЃЈxЉ1ЃЉ+x+1]ЃЈaЮЊШЮвтЪЕЪ§ЃЉЃЎ
ЃЈ1ЃЉЮоТлaШЁКЮжЕЃЌХзЮяЯпCКуЙ§ЖЈЕуЁЁ ЁЁЃЌЁЁ ЁЁЃЎ
ЃЈ2ЃЉЕБaЃН1ЪБЃЌЩшХзЮяЯпCдкЕквЛЯѓЯовРДЮОЙ§ЕФећЪ§ЕуЃЈКсЁЂзнзјБъОљЮЊећЪ§ЕФЕуЃЉЮЊA1ЃЌA2ЃЌЁЁAnЃЌНЋХзЮяЯпCбизХжБЯпyЃНxЃЈxЁн0ЃЉЦНвЦЃЌНЋЦНвЦКѓЕФХзЮяЯпМЧЮЊC nЃЌХзЮяЯпC nОЙ§ЕуAnЃЌC nЕФЖЅЕузјБъЮЊMnЃЈnЮЊе§ећЪ§ЧвnЃН1ЃЌ2ЃЌЁЃЌnЃЌР§ШчnЃН1ЪБЃЌХзЮяЯпC1ОЙ§ЕуA1ЃЌC1ЕФЖЅЕузјБъЮЊM1ЃЉЃЎ
ЂйХзЮяЯпC2ЕФНтЮіЪНЮЊЁЁ ЁЁЃЌЖЅЕузјБъЮЊЁЁ ЁЁЃЎ
ЂкХзЮяЯпC1ЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУPM1ЁЮA2M2ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌВЂХаЖЯЫФБпаЮPM1M2A2ЕФаЮзДЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЂлжБНгаДГіMnЉ1ЃЌMnСНЖЅЕуМфЕФОрРыЃКЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМ1ЪЧвЛИіБеКЯЪБЕФМазгЃЌЭМ2ЪЧИУМазгЕФжїЪгЪОвтЭМЃЌМазгСНБпЮЊACЃЌBDЃЈЕуAгыЕуBжиКЯЃЉЃЌЕуOЪЧМазгзЊжсЮЛжУЃЌOEЁЭACгкЕуEЃЌOFЁЭBDгкЕуFЃЌOE=OF=1cmЃЌAC=BD=6cmЃЌ CE=DFЃЌ CE:AE=2:3.АДЭМЪОЗНЪНгУЪжжИАДМазгЃЌМазгСНБпШЦЕуOзЊЖЏЃЎ
(1)ЕБEЃЌFСНЕуЕФОрРызюДѓжЕЪБЃЌвдЕуAЃЌBЃЌCЃЌDЮЊЖЅЕуЕФЫФБпаЮЕФжмГЄЪЧ_____ cmЃЎ
(2)ЕБМазгЕФПЊПкзюДѓЃЈЕуCгыЕуDжиКЯЃЉЪБЃЌAЃЌBСНЕуЕФОрРыЮЊ_____cmЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЖўДЮКЏЪ§![]() ЭМЯѓЕФЖЅЕуЮЊAЃЌгыyжсНЛгкЕуBЃЌвьгкЖЅЕуAЕФЕуC(1ЃЌn)дкИУКЏЪ§ЭМЯѓЩЯЃЎ
ЭМЯѓЕФЖЅЕуЮЊAЃЌгыyжсНЛгкЕуBЃЌвьгкЖЅЕуAЕФЕуC(1ЃЌn)дкИУКЏЪ§ЭМЯѓЩЯЃЎ
ЃЈ1ЃЉЕБm=5ЪБЃЌЧѓnЕФжЕЃЎ
ЃЈ2ЃЉЕБn=2ЪБЃЌШєЕуAдкЕквЛЯѓЯоФкЃЌНсКЯЭМЯѓЃЌЧѓЕБy![]() ЪБЃЌздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉзїжБЯпACгыyжсЯрНЛгкЕуD.ЕБЕуBдкxжсЩЯЗНЃЌЧвдкЯпЖЮODЩЯЪБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
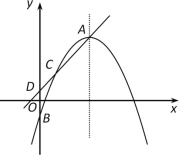
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
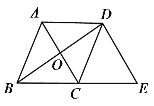
ЁОЬтФПЁПШчЭМЃЌABDФкНггкАыОЖЮЊ5ЕФЁбOЃЌСЌНсAOВЂбгГЄНЛBDгкЕуMЃЌНЛдВЁбOгкЕуCЃЌЙ§ЕуAзїAE//BDЃЌНЛCDЕФбгГЄЯпгкЕуE,AB=AM.
(1)ЧѓжЄЃКABMЁзECA.
(2)ЕБCM=4OMЪБЃЌЧѓBMЕФГЄ.
(3)ЕБCM=kOMЪБЃЌЩшADEЕФУцЛ§ЮЊ![]() , MCDЕФУцЛ§ЮЊ
, MCDЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ(гУКЌkЕФДњЪ§ЪНБэЪО).
ЕФжЕ(гУКЌkЕФДњЪ§ЪНБэЪО).
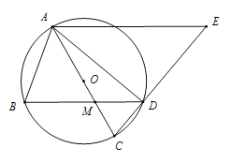
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпLЃКy=ax2+bx+cгыxжсНЛгкAЁЂBЃЈ3ЃЌ0ЃЉСНЕуЃЈAдкBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌвбжЊЖдГЦжсx=1ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпLЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНЋХзЮяЯпLЯђЯТЦНвЦhИіЕЅЮЛГЄЖШЃЌЪЙЦНвЦКѓЫљЕУХзЮяЯпЕФЖЅЕуТфдкЁїOBCФкЃЈАќРЈЁїOBCЕФБпНчЃЉЃЌЧѓhЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшЕуPЪЧХзЮяЯпLЩЯШЮвЛЕуЃЌЕуQдкжБЯпlЃКx=Љ3ЩЯЃЌЁїPBQФмЗёГЩЮЊвдЕуPЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃПШєФмЃЌЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
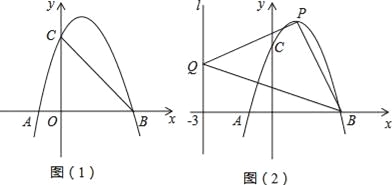
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() НЛзјБъжсгк
НЛзјБъжсгк![]() СНЕуЃЌХзЮяЯп
СНЕуЃЌХзЮяЯп![]() ОЙ§
ОЙ§![]() СНЕуЃЌЧвНЛ
СНЕуЃЌЧвНЛ![]() жсгкСэвЛЕу
жсгкСэвЛЕу![]() .Еу
.Еу![]() ЮЊЕквЛЯѓЯоФкХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§Еу
ЮЊЕквЛЯѓЯоФкХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
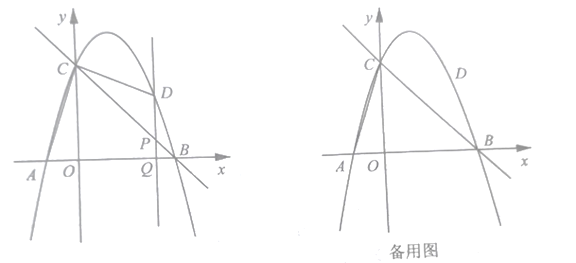
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() дкЕу
дкЕу![]() вЦЖЏЕФЙ§ГЬжаЃЌДцдк
вЦЖЏЕФЙ§ГЬжаЃЌДцдк![]() ЧѓГіДЫЪБ
ЧѓГіДЫЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯШЁЕу![]() дкзјБъЯЕФкШЁЕу
дкзјБъЯЕФкШЁЕу![]() ЮЪЪЧЗёДцдквд
ЮЪЪЧЗёДцдквд![]() ЮЊЖЅЕуЧввд
ЮЊЖЅЕуЧввд![]() ЮЊБпЕФОиаЮЃПШчЙћДцдкЃЌЧыжБНгаДГіЕу
ЮЊБпЕФОиаЮЃПШчЙћДцдкЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com