
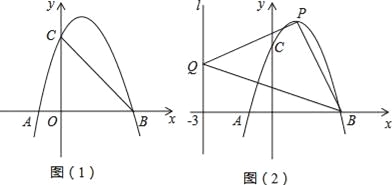
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯLЈєy=ax2+bx+cУлxЦбЅ»УЪAЎўBЈЁ3Ј¬0Ј©БЅµгЈЁAФЪBµДЧуІаЈ©Ј¬УлyЦбЅ»УЪµгCЈЁ0Ј¬3Ј©Ј¬ТСЦЄ¶ФіЖЦбx=1Ј®
ЈЁ1Ј©ЗуЕЧОпПЯLµДЅвОцКЅЈ»
ЈЁ2Ј©Ѕ«ЕЧОпПЯLПтПВЖЅТЖhёцµҐО»і¤¶ИЈ¬К№ЖЅТЖєуЛщµГЕЧОпПЯµД¶ҐµгВдФЪЎчOBCДЪЈЁ°ьАЁЎчOBCµД±ЯЅзЈ©Ј¬ЗуhµДИЎЦµ·¶О§Ј»
ЈЁ3Ј©ЙиµгPКЗЕЧОпПЯLЙПИОТ»µгЈ¬µгQФЪЦ±ПЯlЈєx=©Ѓ3ЙПЈ¬ЎчPBQДЬ·сіЙОЄТФµгPОЄЦ±ЅЗ¶ҐµгµДµИСьЦ±ЅЗИэЅЗРОЈїИфДЬЈ¬Зуіц·ыєПМхјюµДµгPµДЧш±кЈ»ИфІ»ДЬЈ¬ЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎї(1)y=©Ѓx2+2x+3Ј»(2)2ЎЬhЎЬ4Ј»(3)ЈЁ1Ј¬4Ј©Ј¬ЈЁ0Ј¬3Ј©Ј¬ЈЁ![]() Ј¬
Ј¬![]() Ј©єНЈЁ
Ј©єНЈЁ![]() Ј¬
Ј¬![]() Ј©Ј®
Ј©Ј®
ЎѕЅвОцЎїКФМв·ЦОцЈє(1)ЎўАыУГґэ¶ЁПµКэ·ЁЗуіцЕЧОпПЯµДЅвОцКЅјґїЙЈ»(2)ЎўПИЗуіцЦ±ПЯBCЅвОцКЅОЄy=©Ѓx+3Ј¬ФЩЗуіцЕЧОпПЯ¶ҐµгЧш±кЈ¬µГіцµ±x=1К±Ј¬y=2Ј»ЅбєПЕЧОпПЯ¶ҐµгЧшјґїЙµГіцЅб№ыЈ»(3)ЎўЙиPЈЁmЈ¬©Ѓm2+2m+3Ј©Ј¬QЈЁ©Ѓ3Ј¬nЈ©Ј¬УЙ№ґ№Й¶ЁАнµГіцPB2=ЈЁm©Ѓ3Ј©2+ЈЁ©Ѓm2+2m+3Ј©2Ј¬PQ2=ЈЁm+3Ј©2+ЈЁ©Ѓm2+2m+3©ЃnЈ©2Ј¬BQ2=n2+36Ј¬№эPµгЧчPMґ№Ц±УЪyЦбЈ¬Ѕ»yЦбУлMµгЈ¬№эBµгЧчBNґ№Ц±УЪMPµДСУі¤ПЯУЪNµгЈ¬УЙAASЦ¤ГчЎчPQMЎХЎчBPNЈ¬µГіцMQ=NPЈ¬PM=BNЈ¬ФтMQ=©Ѓm2+2m+3©ЃnЈ¬PN=3©ЃmЈ¬µГіц·ЅіМ©Ѓm2+2m+3©Ѓn=3©ЃmЈ¬Ѕв·ЅіМјґїЙЈ®
КФМвЅвОцЈє(1)ЎўЎЯЕЧОпПЯµД¶ФіЖЦбx=1Ј¬BЈЁ3Ј¬0Ј©Ј¬ ЎаAЈЁ©Ѓ1Ј¬0Ј© ЎЯЕЧОпПЯy=ax2+bx+c№эµгCЈЁ0Ј¬3Ј©
Ўаµ±x=0К±Ј¬c=3Ј® УЦЎЯЕЧОпПЯy=ax2+bx+c№эµгAЈЁ©Ѓ1Ј¬0Ј©Ј¬BЈЁ3Ј¬0Ј©
Ўа![]() Ј¬ Ўа
Ј¬ Ўа![]() ЎаЕЧОпПЯµДЅвОцКЅОЄЈєy=©Ѓx2+2x+3Ј»
ЎаЕЧОпПЯµДЅвОцКЅОЄЈєy=©Ѓx2+2x+3Ј»
(2)ЎўЎЯCЈЁ0Ј¬3Ј©Ј¬BЈЁ3Ј¬0Ј©Ј¬ ЎаЦ±ПЯBCЅвОцКЅОЄy=©Ѓx+3Ј¬ ЎЯy=©Ѓx2+2x+3=©ЃЈЁx©Ѓ1Ј©2+4Ј¬
Ўа¶ҐµгЧш±кОЄЈЁ1Ј¬4Ј© ЎЯ¶ФУЪЦ±ПЯBCЈєy=©Ѓx+1Ј¬µ±x=1К±Ј¬y=2Ј»Ѕ«ЕЧОпПЯLПтПВЖЅТЖhёцµҐО»і¤¶ИЈ¬[Фґ:Ўаµ±h=2К±Ј¬ЕЧОпПЯ¶ҐµгВдФЪBCЙПЈ» µ±h=4К±Ј¬ЕЧОпПЯ¶ҐµгВдФЪOBЙПЈ¬
ЎаЅ«ЕЧОпПЯLПтПВЖЅТЖhёцµҐО»і¤¶ИЈ¬К№ЖЅТЖєуЛщµГЕЧОпПЯµД¶ҐµгВдФЪЎчOBCДЪЈЁ°ьАЁЎчOBCµД±ЯЅзЈ©Ј¬
Фт2ЎЬhЎЬ4Ј»
(3)ЎўЙиPЈЁmЈ¬©Ѓm2+2m+3Ј©Ј¬QЈЁ©Ѓ3Ј¬nЈ©Ј¬
ўЩµ±PµгФЪxЦбЙП·ЅК±Ј¬№эPµгЧчPMґ№Ц±УЪyЦбЈ¬Ѕ»yЦбУлMµгЈ¬№эBµгЧчBNґ№Ц±УЪMPµДСУі¤ПЯУЪNµгЈ¬ИзНјЛщКѕЈє ЎЯBЈЁ3Ј¬0Ј©Ј¬ ЎЯЎчPBQКЗТФµгPОЄЦ±ЅЗ¶ҐµгµДµИСьЦ±ЅЗИэЅЗРОЈ¬
ЎаЎПBPQ=90ЎгЈ¬BP=PQЈ¬ ФтЎПPMQ=ЎПBNP=90ЎгЈ¬ЎПMPQ=ЎПNBPЈ¬ ФЪЎчPQMєНЎчBPNЦРЈ¬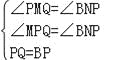 Ј¬
Ј¬
ЎаЎчPQMЎХЎчBPNЈЁAASЈ©Ј¬ ЎаPM=BNЈ¬ ЎЯPM=BN=©Ѓm2+2m+3Ј¬ёщѕЭBµгЧш±кїЙµГPN=3©ЃmЈ¬ЗТPM+PN=6Ј¬
Ўа©Ѓm2+2m+3+3©Ѓm=6Ј¬ ЅвµГЈєm=1»тm=0Ј¬ ЎаPЈЁ1Ј¬4Ј©»тPЈЁ0Ј¬3Ј©Ј®
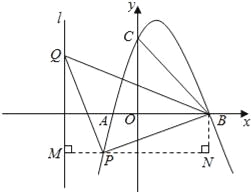
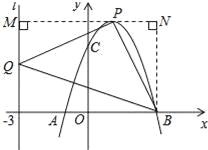
ўЪµ±PµгФЪxЦбПВ·ЅК±Ј¬№эPµгЧчPMґ№Ц±УЪlУЪMµгЈ¬№эBµгЧчBNґ№Ц±УЪMPµДСУі¤ПЯУлNµгЈ¬
Н¬АнїЙµГЎчPQMЎХЎчBPNЈ¬ ЎаPM=BNЈ¬ ЎаPM=6©ЃЈЁ3©ЃmЈ©=3+mЈ¬BNm2©Ѓ2m©Ѓ3Ј¬ Фт3+m=m2©Ѓ2m©Ѓ3Ј¬
ЅвµГm=![]() »т
»т![]() Ј® ЎаPЈЁ
Ј® ЎаPЈЁ![]() Ј¬
Ј¬![]() Ј©»тЈЁ
Ј©»тЈЁ![]() Ј¬
Ј¬![]() Ј©Ј®
Ј©Ј®
ЧЫЙПїЙµГЈ¬·ыєПМхјюµДµгPµДЧш±кКЗЈЁ1Ј¬4Ј©Ј¬ЈЁ0Ј¬3Ј©Ј¬ЈЁ![]() Ј¬
Ј¬![]() Ј©єНЈЁ
Ј©єНЈЁ![]() Ј¬
Ј¬![]() Ј©Ј®
Ј©Ј®


 Гў№ыЅМёЁґп±кІвКФѕнПµБРґр°ё
Гў№ыЅМёЁґп±кІвКФѕнПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬ЕЧОпПЯyЈЅax2©Ѓ![]() x+cЅ»xЦбУЪAЈ¬BБЅµгЈ¬Ѕ»yЦбУЪµгCЈ®Ц±ПЯyЈЅ©Ѓ
x+cЅ»xЦбУЪAЈ¬BБЅµгЈ¬Ѕ»yЦбУЪµгCЈ®Ц±ПЯyЈЅ©Ѓ![]() x+3ѕ№эµгBЈ¬CЈ®
x+3ѕ№эµгBЈ¬CЈ®
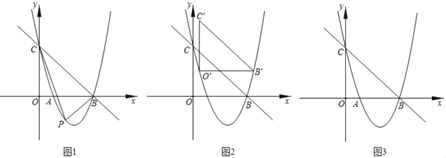
ЈЁ1Ј©ЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©ИфµгPОЄЦ±ПЯBCПВ·ЅµДЕЧОпПЯЙПТ»¶ЇµгЈЁІ»УлµгBЈ¬CЦШєПЈ©Ј¬ФтЎчPBCµДГж»эДЬ№»µИУЪЎчBOCµДГж»эВрЈїИфДЬЈ¬ЗуіцПаУ¦µДµгPµДЧш±кЈ»ИфІ»ДЬЈ¬ЗлЛµГчАнУЙЈ»
ЈЁ3Ј©ИзНј2Ј¬ПЦ°СЎчBOCЖЅТЖЦБИзНјЛщКѕµДО»ЦГЈ¬ґЛК±ИэЅЗРОЛ®ЖЅ·ЅПтТ»±ЯµДБЅёц¶ЛµгµгOЎдУлµгBЎд¶јФЪЕЧОпПЯЙПЈ¬іЖµгOЎдєНµгBЎдОЄЎчBOCФЪЕЧОпПЯЙПµДТ»Ў°їЁµг¶ФЎ±Ј»Из№ы°СЎчBOCРэЧЄТ»¶ЁЅЗ¶ИЈ¬К№µГЖдУа±ЯО»УЪЛ®ЖЅ·ЅПтИ»єуЖЅТЖЈ¬ДЬ№»µГµЅХвёцИэЅЗРОФЪЕЧОпПЯЙПРВµДЎ°їЁµг¶ФЎ±Ј®ЗлЦ±ЅУРґіцЎчBOCФЪТСЦЄЕЧОпПЯЙПЛщУРЎ°їЁµг¶ФЎ±µДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
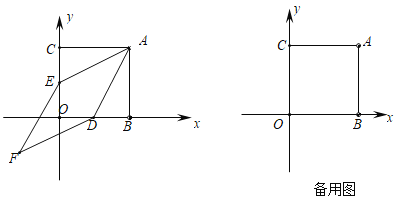
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Хэ·ЅРОABOCµДБЅЦ±ЅЗ±Я·Ц±рФЪЧш±кЦбµДХэ°лЦбЙПЈ¬·Ц±р№эOBЈ¬OCµДЦРµгDЈ¬EЧчAEЈ¬ADµДЖЅРРПЯЈ¬ПаЅ»УЪµгFЈ¬ ТСЦЄOB=8Ј®
ЈЁ1Ј©ЗуЦ¤ЈєЛД±ЯРОAEFDОЄБвРОЈ®
ЈЁ2Ј©ЗуЛД±ЯРОAEFDµДГж»эЈ®
ЈЁ3Ј©ИфµгPФЪxЦбХэ°лЦбЙП(ТмУЪµгD)Ј¬µгQФЪyЦбЙПЈ¬ЖЅГжДЪКЗ·сґжФЪµгGЈ¬К№µГТФµгAЈ¬PЈ¬ QЈ¬GОЄ¶ҐµгµДЛД±ЯРОУлЛД±ЯРОAEFDПаЛЖЈїИфґжФЪЈ¬ЗуµгPµДЧш±кЈ»ИфІ»ґжФЪЈ¬КФЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄEЎўF·Ц±рКЗABCDµД±ЯBCЈ¬ADЙПµДµгЈ¬ЗТBEЈЅDFЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЛД±ЯРОAECFКЗЖЅРРЛД±ЯРОЈ»
ЈЁ2Ј©ИфЛД±ЯРОAECFКЗБвРОЈ¬ЗТBCЈЅ8Ј¬ЎПBACЈЅ90ЎгЈ¬ЗуBEµДі¤Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
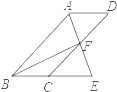
ЎѕМвДїЎїИзНјЈ¬ЛД±ЯРОABCDОЄЖЅРРЛД±ЯРОЈ¬ЎПBADµДЅЗЖЅ·ЦПЯAEЅ»CDУЪµгFЈ¬Ѕ»BCµДСУі¤ПЯУЪµгEЈ®
ЈЁ1Ј©ЗуЦ¤ЈєBE=CDЈ»
ЈЁ2Ј©Б¬ЅУBFЈ¬ИфBFЎНAEЈ¬ЎПBEA=60ЎгЈ¬AB=4Ј¬ЗуЖЅРРЛД±ЯРОABCDµДГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
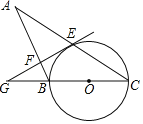
ЎѕМвДїЎїИзНјЈ¬BCКЗЎСOµДЦ±ѕ¶Ј¬CEКЗЎСOµДПТЈ¬№эµгEЧчЎСOµДЗРПЯЈ¬Ѕ»CBµДСУі¤ПЯУЪµгGЈ¬№эµгBЧчBFЎНGEУЪµгFЈ¬Ѕ»CEµДСУі¤ПЯУЪµгAЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЎПABGЈЅ2ЎПCЈ»
ЈЁ2Ј©ИфGFЈЅ3![]() Ј¬GBЈЅ6Ј¬ЗуЎСOµД°лѕ¶Ј®
Ј¬GBЈЅ6Ј¬ЗуЎСOµД°лѕ¶Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
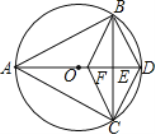
ЎѕМвДїЎїИзНјЈ¬ТСЦЄЎчABCДЪЅУУЪЎСOЈ¬ЗТABЈЅACЈ¬Ц±ѕ¶ADЅ»BCУЪµгEЈ¬FКЗOEЙПµДТ»µгЈ¬CF![]() BDЈ®
BDЈ®
ЈЁ1Ј©ЗуЦ¤ЈєBEЈЅCEЈ»
ЈЁ2Ј©КФЕР¶ПЛД±ЯРОBFCDµДРОЧґЈ¬ІўЛµГчАнУЙЈ»
ЈЁ3Ј©ИфBCЈЅ6Ј¬ADЈЅ10Ј¬ЗуCDµДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіЙМµкµЪТ»ёцФВТФГїјю100ФЄµДјЫёс№єЅш200јюіДЙАЈ¬ТФГїјю150ФЄµДјЫёсКЫуАЈ®УЙУЪКРіЎ»р±¬Ј¬ёГЙМµкµЪ¶юёцФВФЩґО№єЅшТ»ЕъіДЙАЈ¬УлµЪТ»ЕъіДЙАПа±ИЈ¬ХвЕъіДЙАµДЅшјЫєНКэБї¶јУРТ»¶ЁµДМбёЯЈ¬ЖдКэБїµДФці¤ВККЗЅшјЫФці¤ВКµД2.5±¶Ј¬ёГЕъіДЙАИФТФГїјю150ФЄПъКЫЈ®µЪ¶юёцФВЅбКшєуЈ¬ЙМµк¶ФКЈУаµД50јюіДЙАТФГїјю120ФЄµДјЫёсТ»ґОРФЗеІЦПъКЫЈ¬ЙМµкіцКЫХвБЅЕъіДЙА№ІУЇАы17500ФЄЈ®ЙиµЪ¶юЕъіДЙАЅшјЫµДФці¤ВКОЄxЈ®
ЈЁ1Ј©µЪ¶юЕъіДЙАЅшјЫОЄ ФЄЈ¬№єЅшµДКэБїОЄ јюЈ®ЈЁ¶јУГє¬xµДґъКэКЅ±нКѕЈ¬І»Ри»ЇјтЈ©
ЈЁ2Ј©ЗуxµДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЎ°КйПг°Л№рЈ¬ФД¶БФІГОЎ±¶БКй»о¶ЇЦРЈ¬ДіЦРС§ЙиЦГБЛКй·ЁЎў№ъС§ЛР¶БЎўСЭЅІЎўХчОДЛДёц±ИИьПоДїЈЁГїИЛЦ»ІОјУТ»ёцПоДїЈ©Ј¬ѕЕЈЁ2Ј©°аИ«°аН¬С§¶јІОјУБЛ±ИИьЈ¬ёГ°а°аі¤ОЄБЛБЛЅв±ѕ°аН¬С§ІОјУёчПо±ИИьµДЗйїцЈ¬КХјЇХыАнКэѕЭєуЈ¬»жЦЖТФПВІ»НкХыµДХЫПЯНіјЖНјЈЁНј1Ј©єНЙИРОНіјЖНјЈЁНј2Ј©Ј¬ёщѕЭНј±нЦРµДРЕПўЅвґрПВБРёчМвЈє
ЈЁ1Ј©ЗлЗуіцѕЕЈЁ2Ј©И«°аИЛКэЈ»
ЈЁ2Ј©Зл°СХЫПЯНіјЖНјІ№ідНкХыЈ»
ЈЁ3Ј©ДПДПєНДюДюІОјУБЛ±ИИьЈ¬ЗлУГЎ°БР±н·ЁЎ±»тЎ°»КчЧґНј·ЁЎ±ЗуіцЛыГЗІОјУµД±ИИьПоДїПаН¬µДёЕВКЈ®

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com