
【题目】如图,在平面直角坐标系中,直线![]() 交坐标轴于
交坐标轴于![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 两点,且交
两点,且交![]() 轴于另一点
轴于另一点![]() .点
.点![]() 为第一象限内抛物线上一动点,过点
为第一象限内抛物线上一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
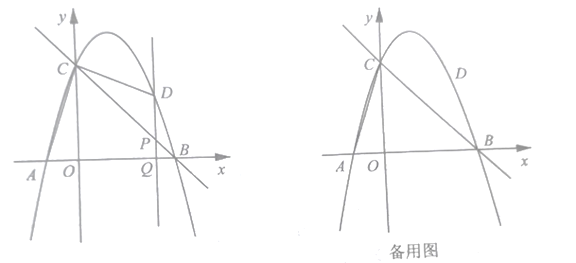
(1)求抛物线的解析式;
(2)设点![]() 的横坐标为
的横坐标为![]() 在点
在点![]() 移动的过程中,存在
移动的过程中,存在![]() 求出此时
求出此时![]() 的值;
的值;
(3)在抛物线上取点![]() 在坐标系内取点
在坐标系内取点![]() 问是否存在以
问是否存在以![]() 为顶点且以
为顶点且以![]() 为边的矩形?如果存在,请直接写出点
为边的矩形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先利用一次函数与坐标轴相交,求出B、C两点的坐标,再根据抛物线解析式及A、B两点坐标设出交点式,再将C的坐标代入求出a的值即可得到抛物线解析式;
(2)如图,过点D作DM⊥BC于M,点P(m,m+3),点D(m,m2+2m+3),利用参数求出DM,CM的长,由锐角三角函数可求解;
(3)分两种情况讨论,当CE⊥BC时或BE⊥BC时,分别求出直线CE的方程或BE的方程,联立方程组可求解.
![]() 直线
直线![]() 交坐标轴于
交坐标轴于![]() 两点,
两点,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
设抛物线的解析式为![]() .
.
将![]() 代入
代入![]() .
.
得![]()
![]() 抛物线解析式为
抛物线解析式为![]() .
.
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,如图1所示
,如图1所示
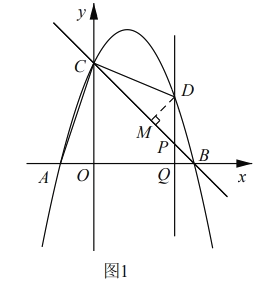
设点![]() 坐标为
坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]()
![]()
![]() .
.
在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]() ,
,
![]()
![]()
![]()
在![]() 中,
中,![]() .
.
![]() 在
在![]() 中,
中,![]()
![]() ,
,
在![]() 中,由勾股定理,
中,由勾股定理,
得![]()
又![]()
![]()
解得![]() (舍去),
(舍去),![]()
![]() 的值为
的值为![]()
(3)存在,
若CE⊥BC时,
∴直线CE解析式为:y=x+3,
∴![]()
∴![]() (舍去)或者
(舍去)或者![]()
∴点E坐标(1,4),
若BE⊥BC时,
∴直线BE解析式为:y=x3,
∴![]()
∴![]() (舍去),或者
(舍去),或者![]()
∴点E坐标(2,5),
综上所述:当点E(1,4)或(2,5)时,以C、B、E、F为顶点且以CB为边的矩形.


科目:初中数学 来源: 题型:
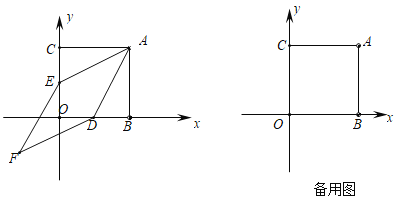
【题目】如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.
(1)求证:四边形AEFD为菱形.
(2)求四边形AEFD的面积.
(3)若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
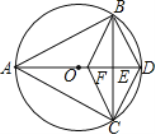
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,CF![]() BD.
BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=6,AD=10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一个月以每件100元的价格购进200件衬衫,以每件150元的价格售罄.由于市场火爆,该商店第二个月再次购进一批衬衫,与第一批衬衫相比,这批衬衫的进价和数量都有一定的提高,其数量的增长率是进价增长率的2.5倍,该批衬衫仍以每件150元销售.第二个月结束后,商店对剩余的50件衬衫以每件120元的价格一次性清仓销售,商店出售这两批衬衫共盈利17500元.设第二批衬衫进价的增长率为x.
(1)第二批衬衫进价为 元,购进的数量为 件.(都用含x的代数式表示,不需化简)
(2)求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励下岗工人再就业,某地市政府规定,企业按成本价提供产品给下岗人员自主销售,成本价与出厂价之间的差价由政府承担.老李按照政策投资销售本市生产的一种儿童面条.已知这种儿童面条的成本价为每袋12元,出厂价为每袋16元,每天销售量![]() (袋)与销售单价
(袋)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)老李在开始创业的第1天将销售单价定为17元,那么政府这一天为他承担的总差价为多少元?
(2)设老李获得的利润为![]() (元),当销售单价为多少元时,每天可获得最大利润?
(元),当销售单价为多少元时,每天可获得最大利润?
(3)物价部门规定,这种面条的销售单价不得高于24元,如果老李想要每天获得的利润不低于216元,那么政府每天为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆的直径,P是半圆与直径AB所围成的图形的外部的一定点,D是直径AB上一动点,连接PD并延长,交半圆于点C,连接AC,BC.已知AB=6 cm,设A,D两点之间的距离为x cm,A,C两点之间的距离为y1 cm,B,C两点之间的距离为y2 cm.
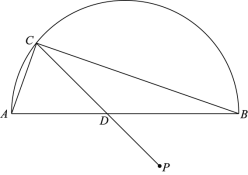
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表自变量x的值进行取点、画图、测量,分别得到y1,y2与x的几组对应值;
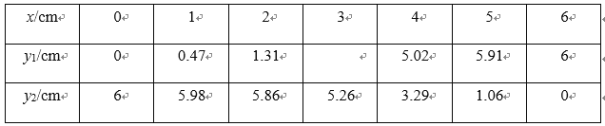
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),
(x, y2),并画出函数y1,y2的图象;
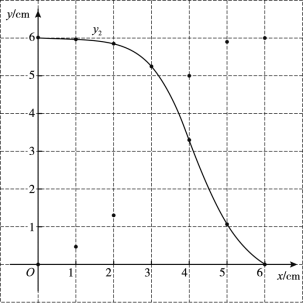
(3)结合函数图象,解决问题:当△ABC有一个角的正弦值为![]() 时,AD的长约为________cm.
时,AD的长约为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF![]() AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.
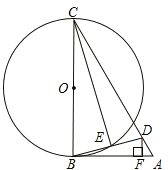
(1)求证:AB是☉O的切线;
(2)若∠A=60°,DF=![]() ,求☉O的直径BC的长。
,求☉O的直径BC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com