
【题目】为鼓励下岗工人再就业,某地市政府规定,企业按成本价提供产品给下岗人员自主销售,成本价与出厂价之间的差价由政府承担.老李按照政策投资销售本市生产的一种儿童面条.已知这种儿童面条的成本价为每袋12元,出厂价为每袋16元,每天销售量![]() (袋)与销售单价
(袋)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)老李在开始创业的第1天将销售单价定为17元,那么政府这一天为他承担的总差价为多少元?
(2)设老李获得的利润为![]() (元),当销售单价为多少元时,每天可获得最大利润?
(元),当销售单价为多少元时,每天可获得最大利润?
(3)物价部门规定,这种面条的销售单价不得高于24元,如果老李想要每天获得的利润不低于216元,那么政府每天为他承担的总差价最少为多少元?
【答案】(1)政府这个月为承担的总差价为156元;(2)当销售单价定为21元时,每月可获得最大利润243元;(3)销售单价定为24元时,政府每个月为他承担的总差价最少为72元.
【解析】
(1)把x=17代入y=3x+90求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;
(2)由总利润=销售量每件纯赚利润,得![]() ,把函数转化成顶点坐标式,根据二次函数的性质求出销售单价及最大利润;
,把函数转化成顶点坐标式,根据二次函数的性质求出销售单价及最大利润;
(3)令![]() ,求出x的值,求出利润的范围,然后根据一次函数的性质求出总差价的最小值.
,求出x的值,求出利润的范围,然后根据一次函数的性质求出总差价的最小值.
解:(1)当![]() 时,
时,![]() ,
,
![]() ,即政府这个月为承担的总差价为156元;
,即政府这个月为承担的总差价为156元;
(2)依题意得,![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最大值243,
有最大值243,
即当销售单价定为21元时,每月可获得最大利润243元;
(3)由题意得:![]() ,解得:
,解得:![]() ,
,
∵![]() ,抛物线开口向下,
,抛物线开口向下,
∴当![]() 时,
时,![]() ,
,
设政府每个月为他承担的总差价为![]() 元,
元,
∴![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 最小
最小![]() ,
,
即销售单价定为24元时,政府每个月为他承担的总差价最少为72元.


科目:初中数学 来源: 题型:
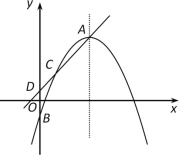
【题目】如图,在平面直角坐标系中,已知二次函数![]() 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
(1)当m=5时,求n的值.
(2)当n=2时,若点A在第一象限内,结合图象,求当y![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
(3)作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
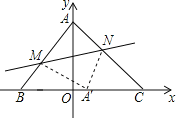
【题目】把△ABC放置在平面直角坐标系中,点A的坐标为(0,8),点B的坐标为(-6,0),点C的坐标为(8,0),M,N分别是线段AB,AC上的点,将△AMN沿直线MN翻折后,点A落在x轴上的A′处.
![]() Ⅰ
Ⅰ![]() 当MN∥x轴时,判断△A'CN的形状.
当MN∥x轴时,判断△A'CN的形状.
![]() Ⅱ
Ⅱ![]() 如图,当A'M⊥AB时.
如图,当A'M⊥AB时.
①求A'的坐标;②求MN的长.
![]() Ⅲ
Ⅲ![]() 当△A'MB是等腰三角形时,直接写出A'的坐标.
当△A'MB是等腰三角形时,直接写出A'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
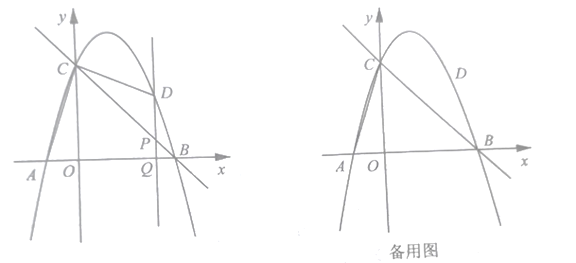
【题目】如图,在平面直角坐标系中,直线![]() 交坐标轴于
交坐标轴于![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 两点,且交
两点,且交![]() 轴于另一点
轴于另一点![]() .点
.点![]() 为第一象限内抛物线上一动点,过点
为第一象限内抛物线上一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 的横坐标为
的横坐标为![]() 在点
在点![]() 移动的过程中,存在
移动的过程中,存在![]() 求出此时
求出此时![]() 的值;
的值;
(3)在抛物线上取点![]() 在坐标系内取点
在坐标系内取点![]() 问是否存在以
问是否存在以![]() 为顶点且以
为顶点且以![]() 为边的矩形?如果存在,请直接写出点
为边的矩形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
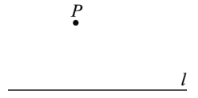
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,

①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:
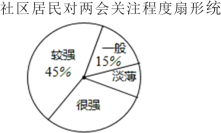
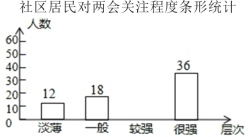
请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图2,则抛物线y=x![]() 的“完美三角形”斜边AB的长________.
的“完美三角形”斜边AB的长________.
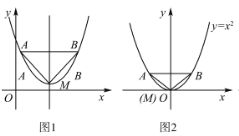
查看答案和解析>>
科目:初中数学 来源: 题型:
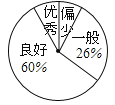
【题目】某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com