
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
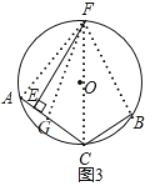
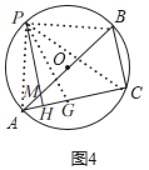
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

【答案】(1)见解析;(2)结论AE=EC+CB不成立,新结论为:CE=BC+AE,见解析;(3)AH的长为![]() ﹣1或
﹣1或![]() +1.
+1.
【解析】
(1)在AC上截取AG=BC,连接FA,FG,FB,FC,证明△FAG≌△FBC,根据全等三角形的性质得到FG=FC,根据等腰三角形的性质得到EG=EC,即可证明.
(2)在CA上截取CG=CB,连接FA,FB,FC,证明△FCG≌△FCB,根据全等三角形的性质得到FG=FB,得到FA=FG,根据等腰三角形的性质得到AE=GE,即可证明.
(3)分点P在弦AB上方和点P在弦AB下方两种情况进行讨论.
解:(1)如图2,
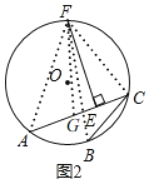
在AC上截取AG=BC,连接FA,FG,FB,FC,
∵点F是![]() 的中点,FA=FB,
的中点,FA=FB,
在△FAG和△FBC中,
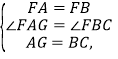
∴△FAG≌△FBC(SAS),
∴FG=FC,
∵FE⊥AC,
∴EG=EC,
∴AE=AG+EG=BC+CE;
(2)结论AE=EC+CB不成立,新结论为:CE=BC+AE,
理由:如图3,
在CA上截取CG=CB,连接FA,FB,FC,
∵点F是![]() 的中点,
的中点,
∴FA=FB,![]() ,
,
∴∠FCG=∠FCB,
在△FCG和△FCB中,
∴△FCG≌△FCB(SAS),
∴FG=FB,
∴FA=FG,
∵FE⊥AC,
∴AE=GE,
∴CE=CG+GE=BC+AE;
(3)在Rt△ABC中,AB=2OA=4,∠BAC=30°,
∴![]()
当点P在弦AB上方时,如图4,
在CA上截取CG=CB,连接PA,PB,PG,
∵∠ACB=90°,
∴AB为⊙O的直径,
∴∠APB=90°,
∵∠PAB=45°,
∴∠PBA=45°=∠PAB,
∴PA=PB,∠PCG=∠PCB,
在△PCG和△PCB中, 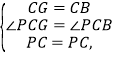
∴△PCG≌△PCB(SAS),
∴PG=PB,
∴PA=PG,
∵PH⊥AC,
∴AH=GH,
∴AC=AH+GH+CG=2AH+BC,
∴![]()
∴![]() 当点P在弦AB下方时,如图5,
当点P在弦AB下方时,如图5,
在AC上截取AG=BC,连接PA,PB,PC,PG
∵∠ACB=90°,
∴AB为⊙O的直径,
∴∠APB=90°,
∵∠PAB=45°,
∴∠PBA=45°=∠PAB,
∴PA=PB,
在△PAG和△PBC中,
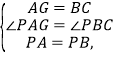
∴△PAG≌△PBC(SAS),
∴PG=PC,
∵PH⊥AC,
∴CH=GH,
∴AC=AG+GH+CH=BC+2CH,
∴![]()
∴![]()
∴![]()
即:当∠PAB=45°时,AH的长为![]() 或
或![]()


科目:初中数学 来源: 题型:
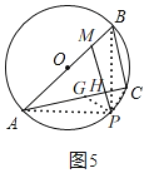
【题目】如图,高高的路灯挂在学校操场旁边上方,高傲而明亮.王刚同学拿起一根![]() 长的竹竿去测量路灯的高度,他走到路灯旁的一个地方,点
长的竹竿去测量路灯的高度,他走到路灯旁的一个地方,点![]() 竖起竹竿(
竖起竹竿(![]() 表示),这时他量了一下竹竿的影长
表示),这时他量了一下竹竿的影长![]() 正好是
正好是![]() ,他沿着影子的方向走,向远处走出两个竹竿的长度(即
,他沿着影子的方向走,向远处走出两个竹竿的长度(即![]() )到点
)到点![]() ,他又竖起竹竿(
,他又竖起竹竿(![]() 表示),这时竹竿的影长
表示),这时竹竿的影长![]() 正好是一根竹竿的长度(即
正好是一根竹竿的长度(即![]() ),此时,王刚同学抬头若有所思地说道:“噢,原来路灯有
),此时,王刚同学抬头若有所思地说道:“噢,原来路灯有![]() 高呀”.你觉得王刚同学的判断对吗?若对,请给出解答,若不对,请说明理由.
高呀”.你觉得王刚同学的判断对吗?若对,请给出解答,若不对,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自卸车车厢的一个侧面是矩形ABCD,AB=3米,BC=0.5米,车厢底部距离地面1.2米.卸货时,车厢倾斜的角度θ=60°,问此时车厢的最高点A距离地面多少米?(精确到1m)
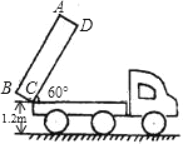
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1ABC的边长为1,正方形A2A1B1C1边长为2.正方形A3A2B2C2边长为4,…依此规律继续做正方形An+1AnBnn,其中点A,A1,A2,A3,…在同一条直线上,连接AC1交A1B1于点D1,连接A1C2交A2B2于点D2,…,若记△AA1D1的面积为S1,△A1A2D2的面积为S2…,△An﹣1AnDn的面积为Sn,则S2019=_____.
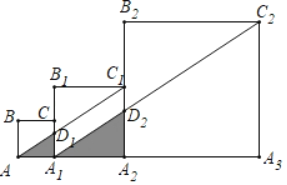
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是边BC上的点,将线段DE绕点E逆时针旋转90°得到EF,过点C作CG∥EF交BA(或其延长线)于点G,连接DF,FG.
(1)FG与CE的数量关系是 ,位置关系是 .
(2)如图2,若点E是CB延长线上的点,其它条件不变.
①(1)中的结论是否仍然成立?请作出判断,并给予证明;
②DE,DF分别交BG于点M,N,若BC=2BE,求![]() .
.
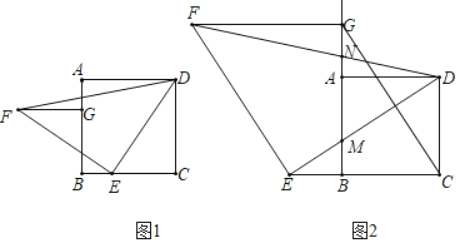
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华在体育馆的看台P处进行观测,测得另一看台观众A处的俯角为15°,观众B处的俯角为60°,已知观众A、B所在看台的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC,PH=15米.
,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC,PH=15米.
(1)AB所在看台坡角∠ABC=____度;
(2)求A、B两点间的距离.(结果精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)
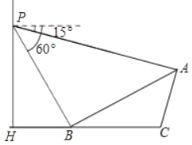
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABB1,△A1B1B2,…,△An﹣2Bn﹣2Bn﹣1,△An﹣1Bn﹣1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn﹣2Bn﹣1,Bn﹣1Bn在同一条直线上,连接ABn交An﹣2Bn﹣1于点P,则PBn﹣1的值为__.
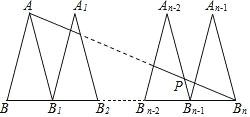
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,点E在AB上,点F在CD上,以EF为折痕,将此矩形折叠,使点A和点C重合,点D和点G重合.
(1)求证:四边形AECF是菱形.
(2)若AB=5,AD=3,则菱形AECF的面积等于_____.
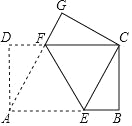
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com