
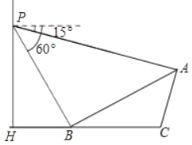
【题目】如图,小华在体育馆的看台P处进行观测,测得另一看台观众A处的俯角为15°,观众B处的俯角为60°,已知观众A、B所在看台的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC,PH=15米.
,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC,PH=15米.
(1)AB所在看台坡角∠ABC=____度;
(2)求A、B两点间的距离.(结果精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8厘米,BC=10厘米,点E在边AB上,且AE=2厘米,如果动点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,动点Q在线段CD上由C点向D点运动,设运动时间为t秒,当△BPE与△CQP全等时,t的值为( )

A. 2B. 1.5或2C. 2.5D. 2或2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
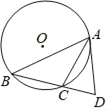
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:∠CAD=∠B.
(2)若AC是∠BAD的平分线,sinB=![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE内接于⊙O点F为![]() 的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
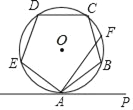
A. 36°B. 54°C. 60°D. 72°
查看答案和解析>>
科目:初中数学 来源: 题型:
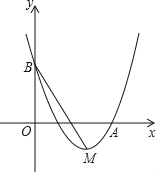
【题目】如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有2个黄球,1个红球和1个白球,除色外都相同.
(1)搅匀后,从袋中随机出一个球,恰好是黄球的概是_____?
(2)搅匀后,从中随机摸出两个球,求摸到一个红球和一个黄球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com