
【题目】如图,正五边形ABCDE内接于⊙O点F为![]() 的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
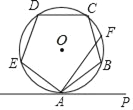
A. 36°B. 54°C. 60°D. 72°
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1ABC的边长为1,正方形A2A1B1C1边长为2.正方形A3A2B2C2边长为4,…依此规律继续做正方形An+1AnBnn,其中点A,A1,A2,A3,…在同一条直线上,连接AC1交A1B1于点D1,连接A1C2交A2B2于点D2,…,若记△AA1D1的面积为S1,△A1A2D2的面积为S2…,△An﹣1AnDn的面积为Sn,则S2019=_____.
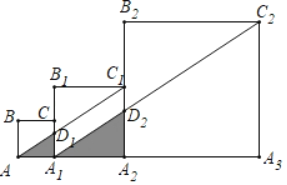
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华在体育馆的看台P处进行观测,测得另一看台观众A处的俯角为15°,观众B处的俯角为60°,已知观众A、B所在看台的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC,PH=15米.
,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC,PH=15米.
(1)AB所在看台坡角∠ABC=____度;
(2)求A、B两点间的距离.(结果精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)
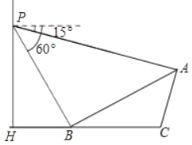
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABB1,△A1B1B2,…,△An﹣2Bn﹣2Bn﹣1,△An﹣1Bn﹣1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn﹣2Bn﹣1,Bn﹣1Bn在同一条直线上,连接ABn交An﹣2Bn﹣1于点P,则PBn﹣1的值为__.
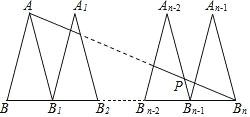
查看答案和解析>>
科目:初中数学 来源: 题型:
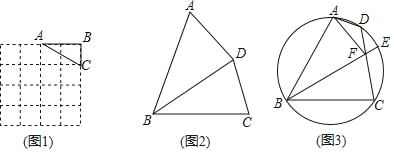
【题目】定义:若一个四边形能被其中的一条对角线分割成两个相似三角形,则称这个四边形为“友谊四边形”.我们熟知的平行四边形就是“友谊四边形”,
(1)如图1,在4×4的正方形网格中有一个Rt△ABC,请你在网格中找格点D,使得四边形ABCD是被AC分割成的“友谊四边形”,(要求画出点D的2种不同位置)
(2)如图2,BD平分∠ABC,BD=4![]() ,BC=8,四边形ABCD是被BD分割成的“友谊四边形”,求AB长;
,BC=8,四边形ABCD是被BD分割成的“友谊四边形”,求AB长;
(3)如图3,圆内接四边形ABCD中,∠ABC=60,点E是![]() 的中点,连结BE交CD于点F,连结AF,∠DAF=30°
的中点,连结BE交CD于点F,连结AF,∠DAF=30°
①求证:四边形ABCF是“友谊四边形”;
②若△ABC的面积为6![]() ,求线段BF的长.
,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
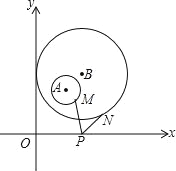
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com