
����Ŀ�������о���ƶ�����ѽ��빥��Σ�ƶ�����Ŵ�ү��ij��λ�İ���£���һƬ�µظ������ֲ������ˮ����ݮ��������ʽ�������ۣ������۵�30���У���һ������20ǧ�ˣ�Ϊ��������������ȡ�˽��۴�ʩ���Ժ�ÿ���ǰһ�������4ǧ�ˣ���x����ۼ�ΪyԪ/ǧ�ˣ�y����x�ĺ�������ʽΪ![]() �ҵ�12����ۼ�Ϊ32Ԫ/ǧ�ˣ���26����ۼ�Ϊ25Ԫ/ǧ�ˣ���֪��ֲ������ݮ�ij�ľ��18Ԫ/ǧ�ˣ�ÿ���������WԪ������=�������멁�ɱ�����
�ҵ�12����ۼ�Ϊ32Ԫ/ǧ�ˣ���26����ۼ�Ϊ25Ԫ/ǧ�ˣ���֪��ֲ������ݮ�ij�ľ��18Ԫ/ǧ�ˣ�ÿ���������WԪ������=�������멁�ɱ�����
��1��m=�� ����n=�� ����
��2����������ݮ�ڼ���ʱ����������������������Ƕ��٣�
��3����������ݮ��30���У�����������870Ԫ�Ĺ��ж����죿
���𰸡���1��m=��![]() ��n=25����2��18��W���=968����3��12��.
��n=25����2��18��W���=968����3��12��.
����������1���������⽫��12����ۼۡ���26����ۼ۴��뼴�ɵ���
��2������1���Ļ����Ϸֶα�ʾ����������ֵ��
��3���ֱ�����2���е���������ȡֵ��Χ������������870��������ע������Ϊ��������
��1������12����ۼ�Ϊ32Ԫ/��������y=mx��76m��
32=12m��76m��
���m=![]() ��
��
����26����ۼ�Ϊ25Ԫ/ǧ��ʱ������y=n��
��n=25��
�ʴ�Ϊ��m=![]() ��n=25��
��n=25��
��2���ɣ�1����x���������Ϊ20+4��x��1��=4x+16��
��1��x��20ʱ��
W=��4x+16����![]() x+38��18��=��2x2+72x+320=��2��x��18��2+968��
x+38��18��=��2x2+72x+320=��2��x��18��2+968��
�൱x=18ʱ��W���=968��
��20��x��30ʱ��W=��4x+16����25��18��=28x+112��
��28��0��
��W��x�������������
�൱x=30ʱ��W���=952��
��968��952��
�൱x=18ʱ��W���=968��
��3����1��x��20ʱ���2x2+72x+320=870��
���x1=25��x2=11��
��������W=��2x2+72x+320�Ŀ���������
��11��x��25ʱ��W��870��
��11��x��20��
��x��������
����9��������870Ԫ��
��20��x��30ʱ����28x+112��870��
���x��27![]() ��
��
��27![]() ��x��30
��x��30
��x��������
����3��������870Ԫ��
����������������������870Ԫ����������12�죮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ԷǸ�������x����������������λ��ֵ��Ϊ<x>����nΪ�Ǹ�����ʱ�����![]() ʱ�� ��<x>=n�����磺<0>��<0.48>��0��<0.64>��<1.493>��1��<2>��2��<3.52>��<4.48>��4���������Խ���������⣺
ʱ�� ��<x>=n�����磺<0>��<0.48>��0��<0.64>��<1.493>��1��<2>��2��<3.52>��<4.48>��4���������Խ���������⣺
��1����գ���<3.49>��__________�������<2a-1>��3����ôa��ȡֵ��Χ��__________��
��2������˵��<x+y>��<x> + <y>���������
��3��������<x>��![]() �����зǸ�������x��ֵ��
�����зǸ�������x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ҫե��֭������ƻ�������֡���������ˮ�������������Ϊ9��7��6��С��ե���֭��ƻ�������֡������Ŀ����ȱ�Ϊ6��3��4����֪С��ե��֭ʱû��ʹ��������������ե��֭ʱ��������ˮ����ʹ�����Σ���������������ȷ����������
A. ֻʹ��ƻ��
B. ֻʹ�ð���
C. ʹ��ƻ�������֣���ʹ�õ�ƻ��������ʹ�õİ��ֿ�����
D. ʹ��ƻ�������֣���ʹ�õİ��ֿ�����ʹ�õ�ƻ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
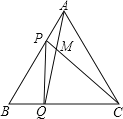
����Ŀ����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ�![]() �ı�AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ���
�ı�AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ���![]() �����˶�ʱ��Ϊt�룮
�����˶�ʱ��Ϊt�룮
![]() ����AQ��CP���ڵ�M������P��Q�˶��Ĺ����У�
����AQ��CP���ڵ�M������P��Q�˶��Ĺ����У�![]() �仯�����仯����˵�����ɣ������䣬��������Ķ�����
�仯�����仯����˵�����ɣ������䣬��������Ķ�����
![]() ����PQ��
����PQ��
![]() ��
��![]() ��ʱ���ж�
��ʱ���ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
![]() ��
��![]() ʱ����
ʱ����![]() ______��
______��![]() ֱ��д�����
ֱ��д�����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AM��BN�ǡ�O���������ߣ�EΪ��O��һ�㣬����E��ֱ��DC�ֱ�AM��BN�ڵ�D��C����CB=CE��
��1����֤��DA=DE��
��2����AB=6��CD=4![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CD��AB������ΪD����E��BC�ϣ�EF��AB������ΪF.
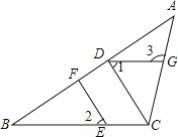
��1��CD��EFƽ����Ϊʲô��
��2�������1=��2��CDƽ����ACB������3=120��������ACB����1�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������7�֣���ͼ����B��F��C��E��һ��ֱ���ϣ�FB=CE��AC=DF���������������������AB=DE���ڡ�A=��D���ۡ�ACB=��DFE��ѡ��һ�����ʵ�������ʹAB��ED������������֤����
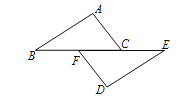
��1��ѡ��������� ������ţ�
��2��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ�����·���Ԫ���ڼ䵽�̳�������䡢���ӻ���ϴ�»������ҵ磬�պø��̳��Ƴ������Żݻ�������Ż�������±���
�����ԭ�ۣ� | �ۿ��Ż� |
������3000Ԫ�IJ��� | ���ۿ��Ż� |
����3000Ԫ��������10000Ԫ���� | �����ۣ� |
����10000Ԫ�IJ��� | ���� |
����ʱ�����������ܵ���������2000Ԫ����160Ԫ�Ż� | |
�磺��ԭ��5000Ԫ����Ʒ��ʵ�ʻ��ѣ�
![]() ��Ԫ��
��Ԫ��
��1����֪���Ź�����������ҵ�ԭ�ۺϼ�Ϊ11500Ԫ�����һ����֧�������������ʵ�ʻ��ѣ�
��2������ڸ��̳�����һ��ԭ��Ϊ![]() Ԫ����Ʒ��
Ԫ����Ʒ��![]() �������ú�
�������ú�![]() �Ĵ���ʽ��ʾʵ�ʻ��ѣ�
�Ĵ���ʽ��ʾʵ�ʻ��ѣ�
��3������ǰ������ͻȻ�뵽�����һ����֧������Ȼ�ۿ��Żݸ���ȴֻ������һ������160Ԫ�Żݣ�������������ҵ�ֿ�֧�����������ϲ�֧������һ������֧�����Ϳ������ܶ������160Ԫ�Żݣ���֪���Ź���ı���ԭ��4800Ԫ�����ӻ�ԭ��4600Ԫ��ϴ�»�ԭ��2100Ԫ������ͨ�������������Ƴ����Żݵ�֧��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC�У���BAC=90����AB=AC����E��AC�ϣ��Ҳ����A��C�غϣ�������ABC���ⲿ����CED��ʹ��CED=90����DE=CE������AD���ֱ���AB��ADΪ�ڱ���ƽ���ı���ABFD������AF��
��1����ֱ��д���߶�AF��AE��������ϵ ��
��2������CED�Ƶ�C��ʱ����ת������E���߶�BC��ʱ����ͼ��������AE�����ж��߶�AF��AE��������ϵ����֤����Ľ��ۣ�
��3����ͼ���Ļ����ϣ�����CED�Ƶ�C������ʱ����ת�����жϣ�2�����еĽ����Ƿ����仯�������䣬���ͼ��д��֤�����̣����仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com