
【题目】对非负有理数x“四舍五入”到个位的值记为<x>.即n为非负整数时,如果![]() 时, 则<x>=n,例如:<0>=<0.48>=0;<0.64>=<1.493>=1;<2>=2;<3.52>=<4.48>=4;……尝试解决下列问题:
时, 则<x>=n,例如:<0>=<0.48>=0;<0.64>=<1.493>=1;<2>=2;<3.52>=<4.48>=4;……尝试解决下列问题:
(1)填空:①<3.49>=__________;②如果<2a-1>=3,那么a的取值范围是__________;
(2)举例说明<x+y>=<x> + <y>不恒成立;
(3)求满足<x>=![]() 的所有非负有理数x的值.
的所有非负有理数x的值.
【答案】(1)①3;②![]() ≤a<
≤a<![]() ;(2)反例见详解;(3)x=0,
;(2)反例见详解;(3)x=0, ![]() ,
, ![]() ,
, ![]() .
.
【解析】
(1) ①根据定义求解可得;②如果精确数是3,那么这个数应在2.5和3.5之间,包含2.5,不包含3.5,让2.5≤2a-1<3.5,解不等式即可;
(2)举个反例即可;
(3) ![]() 为整数,设这个整数为k,这个整数应在k-
为整数,设这个整数为k,这个整数应在k-![]() 和k+
和k+![]() 之间,包含k-
之间,包含k-![]() ,不包含k+
,不包含k+![]() ,求得k的值即可求得所有非负有理数x的值.
,求得k的值即可求得所有非负有理数x的值.
解:(1)①<3.49>=3;
②由题意得,2.5≤2a-1<3.5,
解得:![]() ≤a<
≤a<![]() ,
,
故答案为3;![]() ≤a<
≤a<![]() ;
;
(2)举反例:<0.6>+<0.7>=1+1=2,
而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>,
∴<x+y>=<x> + <y>不恒成立;
(3) ∵x≥0, ![]() 为整数,
为整数,
设![]() =k,k为整数,
=k,k为整数,
则x= ![]() ,
,
∴<![]() >=k,
>=k,
∴k-![]() ≤
≤![]() <k+
<k+![]() ,k≥0,
,k≥0,
∴0≤k≤3,
∴k=0,1,2,3,
∴x=0, ![]() ,
, ![]() ,
, ![]() .
.


科目:初中数学 来源: 题型:
【题目】已知一个三角形纸片的两边长是5和6,第三边的长是方程x2﹣6x+5=0的一个根,若用此三角形纸片剪出一个圆,则剪出的圆的半径最大是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .过点
.过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() .
.
(1)求抛物线的解析式;
(2)若直线![]() 与线段
与线段![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,过
两点,过![]() 点作
点作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,求矩形
,求矩形![]() 的最大面积;
的最大面积;
(3)若直线![]() 将四边形
将四边形![]() 分成左、右两个部分,面积分别为
分成左、右两个部分,面积分别为![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果零售商店分两批次从批发市场共购进“红富士”苹果100箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款400元.
(1)求第一、二次分别购进“红富士”苹果各多少箱?
(2)商店对这100箱“红富士”苹果先按每箱60元销售了75箱后出现滞销,于是决定其余的每箱靠打折销售完.要使商店销售完全部“红富士”苹果所获得的利润不低于1300元,问其余的每箱至少应打几折销售?(注:按整箱出售,利润=销售总收人﹣进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①是一个长为2m,宽为2n的长方形.沿图中虚线把它分割成四块完全相同的小长方形,然后按图②的形状拼成一个正方形.
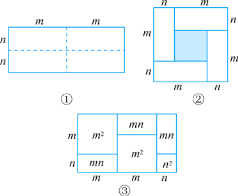
(1)求图②中阴影部分的面积.
(2)观察图②,发现三个代数式(m+n)2,(m-n)2,mn之间的等量关系是 .
(3)若x+y=-6,xy=2.75,求x-y的值.
(4)观察图③,你能得到怎样的代数恒等式?
(5)试画出一个几何图形,使它的面积能表示代数恒等式(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I点为△ABC的内心,D点在BC上,且ID⊥BC,若∠B=44°,∠C=56°,则∠AID的度数为何?( )

A. 174 B. 176 C. 178 D. 180
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com