
【题目】已知一个三角形纸片的两边长是5和6,第三边的长是方程x2﹣6x+5=0的一个根,若用此三角形纸片剪出一个圆,则剪出的圆的半径最大是_____.
【答案】![]()
【解析】先解方程得到x1=1,x2=5,再根据三角形三边的关系得到三角形第三边为5,如图,在△ABC中,AB=AC=5,BC=6,⊙O为△ABC的内切圆,设⊙O的半径为r,作AD⊥BC于D,根据等腰三角形的性质得到BD=CD=3,AD平分∠BAD,根据内心的定义得到点O在AD上,作OE⊥AB于E,OF⊥AC于F,则OD=OE=OF=r,在Rt△ABD中,根据勾股定理得AD=4,然后利用面积法得到![]() ×4×6=
×4×6=![]() ×5r+
×5r+![]() ×6r+
×6r+![]() ×5r,解得r=
×5r,解得r=![]() ,由于三角形的内切圆为三角形内最大的圆,所以此三角形纸片剪出的圆的半径最大值为
,由于三角形的内切圆为三角形内最大的圆,所以此三角形纸片剪出的圆的半径最大值为![]() .
.
x2﹣6x+5=0,
(x﹣1)(x﹣5)=0,
解得x1=1,x2=5,
∵三角形纸片的两边长是5和6,
∴三角形第三边为5,
如图,△ABC中,AB=AC=5,BC=6,⊙O为△ABC的内切圆,设⊙O的半径为r,
作AD⊥BC于D,
则BD=CD=3,AD平分∠BAD,
∴点O在AD上,
作OE⊥AB于E,OF⊥AC于F,则OD=OE=OF=r,
在Rt△ABD中,AD=![]() =4,
=4,
∵S△ABC=S△OAB+S△OBC+S△OAC,
∴![]() ×4×6=
×4×6=![]() ×5r+
×5r+![]() ×6r+
×6r+![]() ×5r,解得r=
×5r,解得r=![]() ,
,
∴此三角形纸片剪出的圆的半径最大值为![]() ,
,
故答案为:![]() .
.



 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】近来爱好跑步的人越来越多,人们对跑步机的需求也越来越大.图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,则跑步机手柄的一端A的高度h四舍五入到0.1m约为( )(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

A. 0.9 B. 1.0 C. 1.1 D. 1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设抛物线![]() 与x轴的交点分别为A、B(点A在点B的左侧),顶点为C.若a、b、c满足
与x轴的交点分别为A、B(点A在点B的左侧),顶点为C.若a、b、c满足![]() ,则称该抛物线为“正定抛物线”;若a、b、c满足
,则称该抛物线为“正定抛物线”;若a、b、c满足![]() ,则称该抛物线为“负定抛物线”.特别地,若某抛物线既是“正定抛物线”又是“负定抛物线”,则称该抛物线为“对称抛物线”.
,则称该抛物线为“负定抛物线”.特别地,若某抛物线既是“正定抛物线”又是“负定抛物线”,则称该抛物线为“对称抛物线”.
(1)“正定抛物线”必经过x轴上的定点___________;“负定抛物线”必经过x轴上的定点___________.
(2)若抛物线![]() 是“对称抛物线”,且△ABC是等边三角形,求此抛物线对应的函数表达式.
是“对称抛物线”,且△ABC是等边三角形,求此抛物线对应的函数表达式.
(3)若抛物线![]() 是“正定抛物线”,设此抛物线交y轴于点D,△BCD的面积为S,求S与b之间的函数关系式.
是“正定抛物线”,设此抛物线交y轴于点D,△BCD的面积为S,求S与b之间的函数关系式.
(4)设“正定抛物线”![]() (b>0)与x轴的交点分别为
(b>0)与x轴的交点分别为![]() 、
、![]() (
(![]() 在
在![]() 的左侧),顶点为M;“负定抛物线”
的左侧),顶点为M;“负定抛物线”![]() (b>0)与x轴的交点分别为
(b>0)与x轴的交点分别为![]() 、
、![]() (
(![]() 在
在![]() 的左侧),顶点为N.在两条抛物线所对应的函数表达式中,当同时满足y随x的增大而增大时的所有x的值在x轴上所对应的点恰好是线段
的左侧),顶点为N.在两条抛物线所对应的函数表达式中,当同时满足y随x的增大而增大时的所有x的值在x轴上所对应的点恰好是线段![]()
![]() (包括端点)时,直接写出此时以M、N、
(包括端点)时,直接写出此时以M、N、![]() 、
、![]() 为顶点的四边形的面积.
为顶点的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开住乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间式(小时)之间的函数图象如图所示,则下列说法中错误的是( )
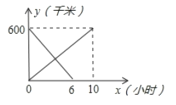
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时,出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且满足
,且满足![]() ,多项式
,多项式![]() 是五次四项式.
是五次四项式.
(1)则![]() 的值为 ,
的值为 ,![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)已知点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 从点
从点![]() 出发,以每秒3个单位的速度向右运动,同时点
出发,以每秒3个单位的速度向右运动,同时点![]() 从点
从点![]() 出发,以每秒4个单位的速度向左运动:
出发,以每秒4个单位的速度向左运动:
①若点![]() 和点
和点![]() 经过
经过![]() 秒后,在数轴上的点
秒后,在数轴上的点![]() 处相遇,求
处相遇,求![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②若点![]() 运动到点
运动到点![]() 处,点
处,点![]() 再出发,则点
再出发,则点![]() 运动几秒后两点之间的距离为8个单位长度.
运动几秒后两点之间的距离为8个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
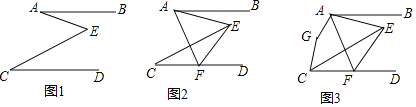
【题目】已知:AB∥CD,平面内有一点E,连接AE、CE
(1)如图1,求证:∠E=∠A+∠C;
(2)如图2,CD上有一点F,连接AF、EF,若∠FAE=∠FEA,∠EFD=2∠C,求证:∠AFC=2∠AEC;
(3)如图3,在(2)的条件下,平面内有一点G,连接AG、CG,若∠GCE与∠GAE互为补角,5∠AFC=2∠G,求∠G的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负有理数x“四舍五入”到个位的值记为<x>.即n为非负整数时,如果![]() 时, 则<x>=n,例如:<0>=<0.48>=0;<0.64>=<1.493>=1;<2>=2;<3.52>=<4.48>=4;……尝试解决下列问题:
时, 则<x>=n,例如:<0>=<0.48>=0;<0.64>=<1.493>=1;<2>=2;<3.52>=<4.48>=4;……尝试解决下列问题:
(1)填空:①<3.49>=__________;②如果<2a-1>=3,那么a的取值范围是__________;
(2)举例说明<x+y>=<x> + <y>不恒成立;
(3)求满足<x>=![]() 的所有非负有理数x的值.
的所有非负有理数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com