
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

【答案】(1)y=x+6;(2)12;(3)![]() (1,
(1,![]() )或
)或![]() (1,5)或
(1,5)或![]() (1,7).
(1,7).
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得:![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=x+6;
(2)在y=x+6中,令x=0,解得:y=6,![]() ;
;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=![]() ,
,
则直线的解析式是:y=![]() x,
x,
当△OMC的面积是△OAC的面积的![]() 时,M的横坐标是
时,M的横坐标是![]() ×4=1,
×4=1,
在y=![]() x中,当x=1时,y=
x中,当x=1时,y=![]() ,则M的坐标是(1,
,则M的坐标是(1,![]() );
);
在y=x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:![]() (1,
(1,![]() )或
)或![]() (1,5).
(1,5).
当M的横坐标是:1,
在y=x+6中,当x=1时,y=7,则M的坐标是(1,7);
综上所述:M的坐标是:![]() (1,
(1,![]() )或
)或![]() (1,5)或
(1,5)或![]() (1,7).
(1,7).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
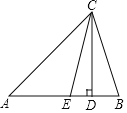
【题目】如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=40°,∠B=76°,求∠DCE的度数;
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示);
(3)当线段CD沿DA方向平移时,平移后的线段与线段CE交于G点,与AB交于H点,若∠A=α,∠B=β,求∠HGE与α、β的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
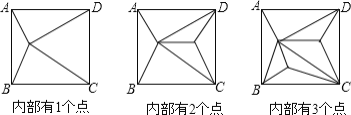
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC与三角形![]() 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形![]() 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.
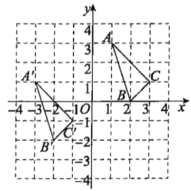
(1)分别写出点![]()
![]()
![]() 的坐标;
的坐标;
(2)说明三角形![]() 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;
(3)若点![]() 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形![]() 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形纸片的两边长是5和6,第三边的长是方程x2﹣6x+5=0的一个根,若用此三角形纸片剪出一个圆,则剪出的圆的半径最大是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
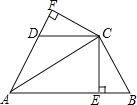
(1)BE与DF是否相等?请说明理由;
(2)若DF=1,AD=3,求AB的长;
(3)若△ABC的面积是23,△ADC面积是18,直接写出△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.
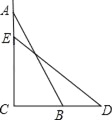
A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com