练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.5米，则梯子顶端A下落了（　　）米．

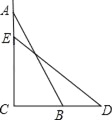
    A. 0.5 B. 1 C. 1.5 D. 2

    【答案】A

    【解析】分析：在直角三角形ABC中，根据勾股定理，得：AC=2米，由于梯子的长度不变，在直角三角形CDE中，根据勾股定理，得CE=1.5米，所以AE=0.5米，即梯子的顶端下滑了0.5米．

    详解：在Rt△ABC中，AB=2.5米，BC=1.5米，

    故AC===2米．

    在Rt△ECD中，AB=DE=2.5米，CD=（1.5+0.5）米，

    故EC===1.5米，

    故AE=AC﹣CE=2﹣1.5=0.5米．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】正方形网格（边长为1的小正方形组成的网格纸，正方形的顶点称为格点）是我们在初中阶段常用的工具，利用它可以解决很多问题．

    （1）如图①中，△ABC是格点三角形（三个顶点为格点），则它的面积为 ；

    （2）如图②，在4×4网格中作出以A为顶点，且面积最大的格点正方形（四个顶点均为格点）；

    （3）人们发现，记格点多边形（顶点均为格点）内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S＝ma＋nb－1，其中m，n为常数．试确定m，n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，D，A，E三点都在直线m上，∠BDA＝∠AEC＝∠BAC，BD＝3，CE＝6，则DE的长为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

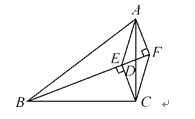
    【题目】如图所示，BD是△ABC的中线，CE⊥BD于点E，AF⊥BD，交BD的延长线于点F.

    (1)试探索BE，BF和BD三者之间的数量关系，并加以证明；

    (2)连接AE，CF，求证：AE∥CF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列结论：w

    ①若a+b+c=0，且abc≠0，则方程a+bx+c=0的解是x=1；

    ②若a（x﹣1）=b（x﹣1）有唯一的解，则a≠b；

    ③若b=2a，则关于x的方程ax+b=0（a≠0）的解为x=﹣；

    ④若a+b+c=1，且a≠0，则x=1一定是方程ax+b+c=1的解；

    其中结论正确个数有（ ）

    A．4个 B．3个 C．2个 D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与x轴、y轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】高铁的开通，给N市市民出行带来了极大的方便，“元旦”期间，甲、乙两人应邀到A市的艺术馆参加演出，甲乘私家车从N市出发1小时后，乙乘坐高铁从N市出发，先到A市火车站，然后再转乘出租车到A市的艺术馆（换车时间忽略不计），两人恰好同时到达A市的艺术馆，他们离开N市的距离y（千米）与乘车时间x（小时）的关系如图所示，请结合图象解答下列问题：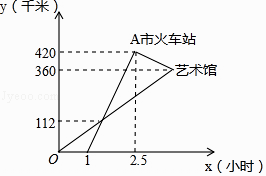
    （1）高铁的平均速度是每小时多少千米？
    （2）分别求甲、乙（乘坐高铁时）两人离开N市的距离y与乘车时间x的函数关系式；
    （3）若甲要提前30分钟到达艺术馆，那么私家车的速度必须达到多少千米/小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A(0，6)，B(b，0)，且b＜0，点C，D分别是OA，AB的中点，△AOB的外角平分线与CD的延长线交于点E.

    (1)求证：∠DAO＝∠DOA；

    (2)①若b＝－8，求CE的长；

    ②若CE＝＋1，则b＝________．

    (3)是否存在这样的b值，使得四边形OBED为平行四边形？若存在，请求出此时四边形OBED对角线的交点坐标；若不存在，请说明理由．

    (4)直线AE与x轴交于点F，请用含b的式子直接写出点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点P是AB下方的半圆上不与点A，B重合的一个动点，点C为AP中点，延长CO交⊙O于点D，连接AD，过点D作⊙O的切线交PB的廷长线于点E，连CE交AB于点F，连接DF．
    （1）求证：△DAC≌△ECP；
    （2）填空： ①四边形ACED是何种特殊的四边形？
    ②在点P运动过程中，线段DF、AP的数量关系是 ．

    查看答案和解析>>

    同步练习册答案