
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
【答案】![]()
【解析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.
解:在△ABE和△ACF中,
∠E=∠F=90°,AE=AF,∠B=∠C,
∴△ABE≌△ACF,
∴∠EAB=∠FAC,AE=AF,AB=AC,
∴∠EAB-∠MAN=∠FAC-∠NAM,即∠EAM=∠FAN,
在△AEM和△AFN中,
∠E=∠F=90°,AE=AF,∠EAM=∠FAN,
∴△AEM≌△AFN,
∴EM=FN,∠FAN=∠EAM,故选项①和③正确;
在△ACN和△ABM中,
∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),
∴△ACN≌△ABM,故选项④正确;
若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,
则正确的选项有:①③④.
故答案为:①③④


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且满足
,且满足![]() ,多项式
,多项式![]() 是五次四项式.
是五次四项式.
(1)则![]() 的值为 ,
的值为 ,![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)已知点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 从点
从点![]() 出发,以每秒3个单位的速度向右运动,同时点
出发,以每秒3个单位的速度向右运动,同时点![]() 从点
从点![]() 出发,以每秒4个单位的速度向左运动:
出发,以每秒4个单位的速度向左运动:
①若点![]() 和点
和点![]() 经过
经过![]() 秒后,在数轴上的点
秒后,在数轴上的点![]() 处相遇,求
处相遇,求![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②若点![]() 运动到点
运动到点![]() 处,点
处,点![]() 再出发,则点
再出发,则点![]() 运动几秒后两点之间的距离为8个单位长度.
运动几秒后两点之间的距离为8个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
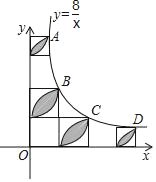
【题目】已知,A、B、C、D是反比例函数y=![]() (x>0)图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是__________(用含π的代数式表示).
(x>0)图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是__________(用含π的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负有理数x“四舍五入”到个位的值记为<x>.即n为非负整数时,如果![]() 时, 则<x>=n,例如:<0>=<0.48>=0;<0.64>=<1.493>=1;<2>=2;<3.52>=<4.48>=4;……尝试解决下列问题:
时, 则<x>=n,例如:<0>=<0.48>=0;<0.64>=<1.493>=1;<2>=2;<3.52>=<4.48>=4;……尝试解决下列问题:
(1)填空:①<3.49>=__________;②如果<2a-1>=3,那么a的取值范围是__________;
(2)举例说明<x+y>=<x> + <y>不恒成立;
(3)求满足<x>=![]() 的所有非负有理数x的值.
的所有非负有理数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元;实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,预计二期工程完成后每月将产生不少于1300吨污水,请你求出用于二期工程的污水处理设备的所有购买方案.
(3)经测算:每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.在(2)中的方案中,哪种购买方案使得设备的各种维护费和电费总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
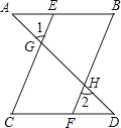
【题目】完善下列解题步辈.井说明解题依据.
如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
证明:∵∠1=∠2(已知)
且∠1=∠CGD(______)
∴∠2=∠CGD(______)
∴______∥______(______),
∴∠C=______(______)
又∵∠B=∠C(已知)
∴______=∠B
AB∥CD(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的宣传单为莱克印刷公司设计与印刷卡片计价方式的说明,妮娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的2成?( )

A. 112 B. 121 C. 134 D. 143
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?( )
A. 只使用苹果
B. 只使用芭乐
C. 使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多
D. 使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.
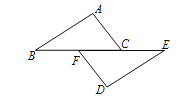
(1)选择的条件是 (填序号)
(2)证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com