练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（本题7分）如图，点B、F、C、E在一条直线上，FB=CE，AC=DF，请从下列三个条件：①AB=DE；②∠A=∠D；③∠ACB=∠DFE中选择一个合适的条件，使AB∥ED成立，并给出证明．

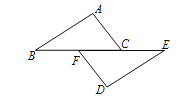
    （1）选择的条件是 （填序号）

    （2）证明：

    【答案】（1）选择①AB=ED或③∠ACB=∠DFE；（2）证明①；证明见试题解析．

    【解析】

    试题分析：（1）利用全等三角形的判定定理选出合适的条件即可；

    （2）利用SSS进而判断出全等三角形，得出AB∥ED即可．

    试题解析：（1）选择①AB=ED或③∠ACB=∠DFE即可；

    （2）∵FB=CE，∴BC=EF，

    在△ABC和△EFD中，∵AB=ED，AC=DF，BC=EF，∴△ABC≌△EFD（SSS），∴∠B=∠E，∴AB∥ED．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知线段AB的两个端点分别是A（﹣4，﹣1），B（1，1），将线段AB平移得到线段A′B′，若点A′的坐标为（﹣2，2），则点B′的坐标为（　　）

    A. （3，4） B. （4，3） C. （﹣1，﹣2） D. （﹣2，﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了丰富学生的课外活动，拓展孩子们的课外视野，我校的社团活动每年都在增加，社员也一直在增加．2017年我校八年级社员的总人数是300人，2019年我校八年级总校社员有432人。试求出这两年八年级社员人数的平均增长率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

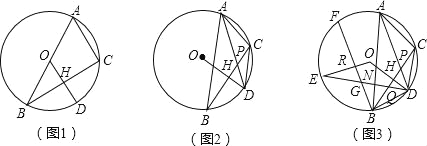
    【题目】已知：△ABC内接于⊙O，D是弧BC上一点，OD⊥BC，垂足为H．

    （1）如图1，当圆心O在AB边上时，求证：AC=2OH；

    （2）如图2，当圆心O在△ABC外部时，连接AD、CD，AD与BC交于点P，求证：∠ACD=∠APB；

    （3）在（2）的条件下，如图3，连接BD，E为⊙O上一点，连接DE交BC于点Q、交AB于点N，连接OE，BF为⊙O的弦，BF⊥OE于点R交DE于点G，若∠ACD﹣∠ABD=2∠BDN，AC=，BN=，tan∠ABC=，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列实数中，最小的数是（ ）

    A.﹣2B.2C.3D.﹣3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在扇形统计图中，其中一个扇形的中心角为72°，则这个扇形所表示的部分占总体的百分数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.一个直角三角形一定不是等腰三角形

    B.一个钝角三角形一定不是等腰三角形

    C.一个等腰三角形一定不是锐角三角形

    D.一个等边三角形一定不是钝角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知m2﹣mn=7，mn﹣n2=﹣2，求m2﹣n2及m2﹣2mn+n2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品的价格标签已丢失，售货员只知道“它的进价为90元，打七折出售后，仍可获利5%”，你认为售货员应标在标签上的价格为元．

    查看答案和解析>>

    同步练习册答案