
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为![]() ,直线的解析式为
,直线的解析式为![]() .(2)
.(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
(1)依题意得: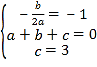 ,解得:
,解得: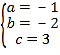 ,
,
∴抛物线的解析式为![]() .
.
∵对称轴为![]() ,且抛物线经过
,且抛物线经过![]() ,
,
∴把![]() 、
、![]() 分别代入直线
分别代入直线![]() ,
,
得![]() ,解之得:
,解之得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
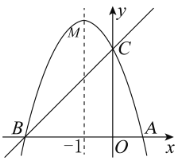
(2)直线![]() 与对称轴
与对称轴![]() 的交点为
的交点为![]() ,则此时
,则此时![]() 的值最小,把
的值最小,把![]() 代入直线
代入直线![]() 得
得![]() ,
,
∴![]() .即当点
.即当点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小时
的距离之和最小时![]() 的坐标为
的坐标为![]() .
.
(注:本题只求![]() 坐标没说要求证明为何此时
坐标没说要求证明为何此时![]() 的值最小,所以答案未证明
的值最小,所以答案未证明![]() 的值最小的原因).
的值最小的原因).
(3)设![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
①若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
②若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
③若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:
![]() ,
,![]() .
.
综上所述![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0
(Ⅰ)当m=![]() 时,求方程的实数根;
时,求方程的实数根;
(Ⅱ)若方程有两个不相等的实数根,求实数m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)64的展开式中第三项的系数为( )
A. 2016 B. 2017 C. 2018 D. 2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
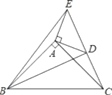
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交,当y2≤y3时,利用图象写出此时x的取值范围是( )
A. x≤﹣1 B. x≥3 C. ﹣1≤x≤3 D. x≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
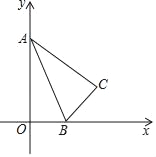
【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
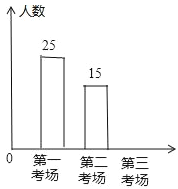
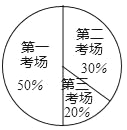
【题目】2017年12月全市组织了计算机等级考试,江南中学九(1)班同学都参加了计算机等级考试,分第一试场、第二试场、第三试场,下面两幅统计图反映原来安排九(1)班考生人数,请你根据图中的信息回答下列问题:
(1)该班参加第三试场考试的人数为_____,并补全频数分布直方图;
(2)根据实际情况,需从第一试场调部分学生到第三试场考试,使第一试场的人数与第三试场的人数比为2:3,应从第一试场调多少学生到第三试场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
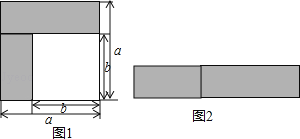
(1)如图1,阴影部分的面积是 (写成平方差的形式);
(2)如图2,若将阴影部分裁剪后重新拼成一个长方形,它的宽是 长是 ,面积可表示为 (写成多项式乘法的形式).
(3)运用以上得到的公式,计算:(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com