
【题目】将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交,当y2≤y3时,利用图象写出此时x的取值范围是( )
A. x≤﹣1 B. x≥3 C. ﹣1≤x≤3 D. x≥0
科目:初中数学 来源: 题型:
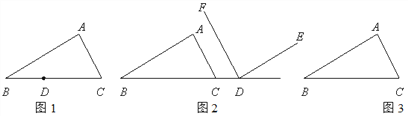
【题目】已知:△ABC和同一平面内的点D.
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
① 依题意,在图1中补全图形;
② 判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
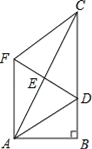
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
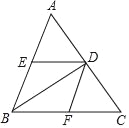
【题目】如图,在△ABC中,DF∥AB,DE∥BC,连接BD.
(1)求证:△DEB≌△BFD;
(2)若点D是AC边的中点,当△ABC满足条件_____时,四边形DEBF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
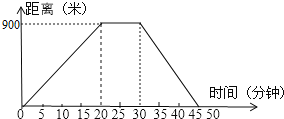
【题目】如图,反映了小明从家里到超市的时间与距离之间关系的一幅图。
(1)图中自变量和因变量各是什么?
(2)小明到达超市用了多少时间?超市离家多远?
(3)分别求小明从家里到超市时的平均速度是多少?返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学课上,老师要求学生根据图中李亮与张鑫的对话内容,展开如下活动:
仔细阅读对话内容:

活动:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,他需要付多少钱;
(2)你认为购买多少元钱的书时办卡与不办卡花费相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在期末考试来临之际,同学们都进入紧张的复习阶段,为了了解同学们晚上的睡眠情况,现对年级部分同学进行了调查统计,并制成如下两幅不完整的统计图:(其中A代表睡眠时间8小时左右,B代表睡眠时间6小时左右,C代表睡眠时间4小时左右,D代表睡眠时间5小时左右,E代表睡眠时间7小时左右),其中扇形统计图中“E”的圆心角为90°,请你结合统计图所给信息解答下列问题:
(1)共抽取了 名同学进行调查,同学们的睡眠时间的中位数是 小时左右,并将条形统计图补充完整;
(2)请你估计年级每个学生的平均睡眠时间约多少小时?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com