
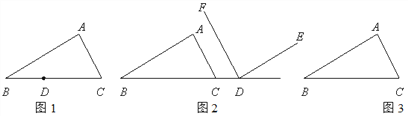
����Ŀ����֪����ABC��ͬһƽ���ڵĵ�D��
��1����ͼ1����D��BC���ϣ���D��DE��BA��AC��E��DF��CA��AB��F��
�� �����⣬��ͼ1�в�ȫͼ�Σ�
�� �жϡ�EDF���A��������ϵ����ֱ��д�����ۣ�����֤������
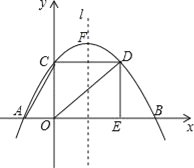
��2����ͼ2����D��BC���ӳ����ϣ�DF��CA����EDF=��A���ж�DE��BA��λ�ù�ϵ����֤����
��3����ͼ3����D�ǡ�ABC�ⲿ��һ�����㣬��D��DE��BA��ֱ��AC��E��DF��CA��ֱ��AB��F��ֱ��д����EDF���A��������ϵ������֤������
���𰸡���1���� ��ȫͼ�μ��������� ��EDF=��A��
��2��DE��BA��֤����������
��3����EDF=��A����EDF+��A=180��
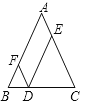
�������������������1���������ⲹȫͼ�μ��ɣ�����ƽ���ı��ε��ж��ɵ��ı���AEDF��ƽ���ı��Σ�����ƽ���ı��ζԽ���ȵý������2���ӳ�BA����ƽ���ߵ����ʵá�2=��3�����������á�1=��3�����ڴ��������ֱ��ƽ�е�DE��BA����3����������ۼ���.
�����������1���� ��ȫͼ�����£�
 ��
��
�� ��EDF=��A.
��DE��BA��DF��CA
���ı���AEDF��ƽ���ı���
���EDF=��A
��2��DE��BA.
֤������ͼ���ӳ�BA��DF��G.
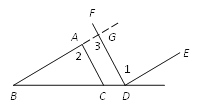
�� DF��CA��
�� ��2=��3.
�֡� ��1=��2��
�� ��1=��3.
�� DE��BA
��3���ɣ�2��֪��EDF=��A��
������D����λ��ʱ��
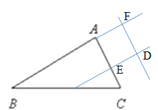
���ı���AEDF��ƽ���ı��Σ�
���BAC=��AFD, ��AFD+��EDF=180��,
���EDF+��BAC=180��


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̽����
��1���������ϵĵ�P�������²������Ȱѵ�P��ʾ��������![]() ���ٰ���������Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P�䣮
���ٰ���������Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P�䣮
��A��B�������ϣ����߶�AB�ϵ�ÿ�����������������õ��߶�A��B�䣬���е�A��B�Ķ�Ӧ��ֱ�ΪA�䣬B�䣮��ͼ1������A��ʾ�����ǩ�3�����A���ʾ�������� ��������B���ʾ������2�����B��ʾ�������� ������֪�߶�AB�ϵĵ�E��������������õ��Ķ�Ӧ��E�����E�غϣ����E��ʾ�������� ����

��2����ͼ2����ƽ��ֱ������ϵxOy�У���������ABCD�����ڲ���ÿ����������²�������ÿ����ĺᡢ�����궼����ͬһ��ʵ��a�����õ��ĵ�������ƽ��m����λ��������ƽ��n����λ��m��0��n��0�����õ�������A��B��C��D�估���ڲ��ĵ㣬���е�A��B�Ķ�Ӧ��ֱ�ΪA�䣬B�䣮��֪������ABCD�ڲ���һ����F��������������õ��Ķ�Ӧ��F�����F�غϣ����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��![]()
��2��20132��2012��2014�������㣩
��3����3a2��3+a2a4��a8��a2
��4����x��2����3x��1��
��5����x��1����x+1������x+2��2
��6����a+3b��2c����a��3b��2c��
��7����m��2n+1��2
��8����2a��3b��2��2a+3b��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά������Ȩ�棬���齨�Ĺ��Һ���ּӴ������Ϻ���Ѳ�����ȡ�һ�죬�����Һ��ബ�պ�����ij�������������ϵ�A��B����Ѳ�ߣ�ͬʱ����һ�Ҳ��������Ĵ�ֻͣ��C��������ͼ��ʾ��AB��60![]() �����B�����C�ڱ�ƫ��45�ķ����ϣ�A�����C�ڱ�ƫ��30�ķ����ϣ��ں�����AB����һ����D�����AD��120
�����B�����C�ڱ�ƫ��45�ķ����ϣ�A�����C�ڱ�ƫ��30�ķ����ϣ��ں�����AB����һ����D�����AD��120![]() ���
���

��1���ֱ����A��C��B��C�ľ���AC��BC������������ţ�
��2����֪�ڵ���D��Χ100���ﷶΧ���а���Ⱥ������A�����ബ��ACǰ��C���̲飬;����������Σ�գ���������������������������������������������������
���ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.45��
��2.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����г���x�������������������ÿ��ᣬ��ÿ��������5�ˣ�����һ������ֻ��2�ˣ����ճ�6�����Σ������ṩ����Ϣ�������ú�x��ʽ�ӱ�ʾ��ָ���г���ʽ���ǵ���ʽ���Ƕ���ʽ���������x��70ʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬BC=6cm��AC=8cm����P�ӵ�C��ʼ������CA������1cm/s���ٶ��˶���ͬʱ����QҲ�ӵ�C��ʼ������CB������3cm/s���ٶ��˶�.
��1���������PCQ�����Ϊ3cm2����ʱPQ�ij��Ƕ��٣�������������θ�ʽ��ʾ��
��2���������A��B��P��QΪ������ı��ε����Ϊ22cm2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
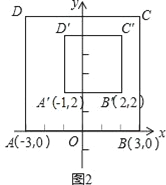
����Ŀ����ͼ����֪������y=ax2+bx+c������A����3��0����B��9��0����C��0��4����CD��ֱ��y�ᣬ���������ڵ�D��DE��ֱ��x�ᣬ����ΪE��l�������ߵĶԳ��ᣬ��F�������ߵĶ��㣮
��1��������κ����ı���ʽ�Լ���D�����ꣻ
��2����Rt��AOC��x������ƽ�Ƶ���ֱ�DZ�OC��Գ���l�غϣ����ضԳ���l����ƽ�Ƶ���C���F�غϣ��õ�Rt��A1O1F�����ʱRt��A1O1F�����OCDE�ص����ֵ�ͼ�ε������
��3����Rt��AOC��x������ƽ��t����λ���ȣ�0��t��6���õ�Rt��A2O2C2��Rt��A2O2C2��Rt��OED�ص����ֵ�ͼ�������ΪS����S��t֮��ĺ�������ʽ����д���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com