
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

【答案】(1)![]() 秒后△PCQ的面积为3平方厘米,此时PQ的长是
秒后△PCQ的面积为3平方厘米,此时PQ的长是![]() ;
;
(2)经过![]() 秒或
秒或![]() 秒,以A、B、P、Q为顶点的四边形的面积为22cm2
秒,以A、B、P、Q为顶点的四边形的面积为22cm2
【解析】试题分析:(1)根据题意∠C=90°,可以得出△PCQ的面积为![]() ×PC×CQ,设出t秒后满足要求,则根据△PCQ的面积是3 cm2列出等量关系求出t的值即可.
×PC×CQ,设出t秒后满足要求,则根据△PCQ的面积是3 cm2列出等量关系求出t的值即可.
(2)根据四边形ABQP的面积=SΔABC-SΔPCQ,列式计算即可.
试题解析:(1)设t秒后△PCQ的面积为3平方厘米,
则有PC=t cm,CQ=3t cm,
依题意,得: ![]() t×3t=3,
t×3t=3,
![]()
![]() (舍去)
(舍去)
由勾股定理,得:PQ=![]()
答: ![]() 秒后△PCQ的面积为3平方厘米,此时PQ的长是
秒后△PCQ的面积为3平方厘米,此时PQ的长是![]()
(2)① 当P在线段AC上,Q在线段BC上时, ![]()
S四边形APQB= S△ABC﹣S△PQC
![]()
![]() ,
,
得![]() (舍去)
(舍去)
② 当P在线段AC上,Q在线段BC延长线上时, ![]()
S四边形APBQ= S△AQC﹣S△PBC=![]()
![]() ,得
,得![]()
③ 当P在线段AC的延长线上,Q在线段BC延长线上时, ![]()
S四边形ABQP= S△PQC﹣S△ABC=![]()
![]() (不符合题意,舍去),(或者得
(不符合题意,舍去),(或者得![]() ,
, ![]() ,都不符合题意,舍去)
,都不符合题意,舍去)
综上: ![]() 或
或![]()
答,经过![]() 秒或
秒或![]() 秒,以A、B、P、Q为顶点的四边形的面积为22cm2
秒,以A、B、P、Q为顶点的四边形的面积为22cm2


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系内,将函数y=2(x+1)2﹣1的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
A. (﹣1,1)B. (1,﹣2)C. (2,﹣2)D. (1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
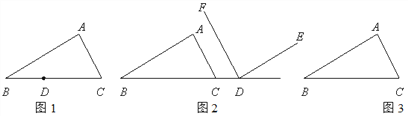
【题目】已知:△ABC和同一平面内的点D.
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
① 依题意,在图1中补全图形;
② 判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
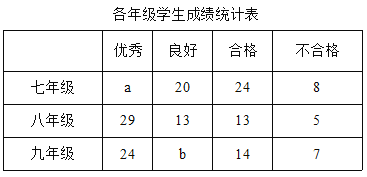

根据以上信息解决下列问题:
(1)在统计表中,a的值为 ,b的值为 ;
(2)在扇形统计图中,八年级所对应的扇形圆心角为 度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“十一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31=465(万元),你认为这样推断是否合理?答:________________.(选填“合理”或“不合理”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程2x2=1-3x化成ax2+bx+c=0的形式后,a、b、c的值分别为( )
A. 2,1,-3 B. 2,3,-1 C. 2,3,1 D. 2,1,3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com