
【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
【答案】 ![]() π 8
π 8![]() ﹣12
﹣12
【解析】(1)根据直角三角形斜边中线等于斜边一半,确定中点P的运动路径:以O为圆心,以OP为半径的![]() 圆弧,半径OP=
圆弧,半径OP=![]() AB=2
AB=2![]() ,代入周长公式计算即可;
,代入周长公式计算即可;
(2)分为两种情况:
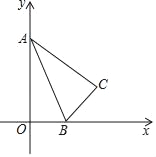
①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,点C运动的路径长是CC′的长;
②当A再继续向上移动,直到点B与O重合时,如图3,此时点C运动的路径是从C′到C,长是CC′;
分别计算并相加.
(1)如图1.
∵∠AOB=90°,P为AB的中点,∴OP=![]() AB.
AB.
∵AB=4![]() ,∴OP=2
,∴OP=2![]() ,∴AB中点P运动的轨迹是以O为圆心,以OP为半径的
,∴AB中点P运动的轨迹是以O为圆心,以OP为半径的![]() 圆弧,即AB中点P经过的路径长=
圆弧,即AB中点P经过的路径长=![]() ×2×2
×2×2![]() π=
π=![]() π;
π;
(2)①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,点C运动的路径长是CC′的长,∴AC′=OC=8.
∵AC′∥OB,∴∠AC′O=∠COB,∴cos∠AC′O=cos∠COB=![]() =
=![]() =
=![]() ,∴OC′=4
,∴OC′=4![]() ,∴CC′=4
,∴CC′=4![]() ﹣8;
﹣8;
②当A再继续向上移动,直到点B与O重合时,span>如图3,此时点C运动的路径是从C′到C,长是CC′,CC′=OC′﹣BC=4![]() ﹣4.
﹣4.
综上所述:点C运动的路径长是:4![]() ﹣8+4
﹣8+4![]() ﹣4=8
﹣4=8![]() ﹣12;
﹣12;
故答案为:(1)![]() π; (2)8
π; (2)8![]() ﹣12.
﹣12.


科目:初中数学 来源: 题型:
【题目】定义:如果![]() ,那么称b为n的布谷数,记为
,那么称b为n的布谷数,记为![]() .
.
例如:因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以![]() .
.
(1)根据布谷数的定义填空:g(2)=________________,g(32)=___________________.
(2)布谷数有如下运算性质:
若m,n为正整数,则![]() ,
,![]() .
.
根据运算性质解答下列各题:
①已知![]() ,求
,求![]() 和
和![]() 的值;
的值;
②已知![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOE=90°.
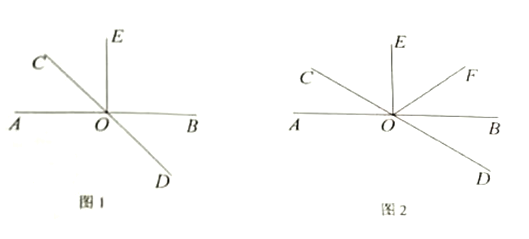
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对任意一个两位数![]() ,如果
,如果![]() 满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为
满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为![]() .例如:
.例如:![]() ,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以
,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以![]() .根据以上定义,回答下列问题:
.根据以上定义,回答下列问题:
(1)填空:①下列两位数:40,42,44中,“迥异数”为_______;②计算:![]() =_______;
=_______;
(2)如果一个“迥异数”![]() 的十位数字是
的十位数字是![]() ,个位数字是
,个位数字是![]() ,且
,且![]() ,请求出“迥异数”
,请求出“迥异数”![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )

A.1.5B.1.8C.2D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的20个小球,其中红球6个,黑球14个
(1)先从袋子中取出x(x>3)个红球后,再从袋子中随机摸出1个球,将“摸出黑球”,记为事件A.请完成下列表格.
事件A | 必然事件 | 随机事件 |
x的值 |
(2)先从袋子中取出m个红球,再放入2m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
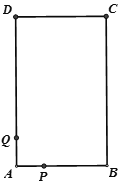
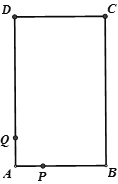
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com