
【题目】已知点![]() 的坐标为
的坐标为![]() .
.
(1)若点![]() 在
在![]() 轴上,求
轴上,求![]() 点坐标.
点坐标.
(2)若点P到两坐标轴的距离相等,求点P的坐标.
【答案】(1)点P的坐标为(0,12);(2)点P的坐标为(3,3)或(6,-6).
【解析】
(1)由点P在y轴上可知点P的横坐标为0,据此求得a的值即可求得答案;
(2)由于点P的坐标为(2-a,3a+6),且到两坐标轴的距离相等,则可得|2-a|=|3a+6|,然后去绝对值得到关于a的两个一次方程,再解方程即可.
(1)由题意得:2-a=0,
解得:a=2,
3a+6=12,
所以点P的坐标为(0,12);
(2)根据题意得|2-a|=|3a+6|,
所以2-a=3a+6或2-a=-(3a+6),
解得a=-1或a=-4,
当a=-1时,2-a=3,3a+6=3,所以点P坐标为(3,3);
当a=-4时,2-a=6,3a+6=-6,所以点P坐标为(6,-6),
综上点P的坐标为(3,3)或(6,-6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】足球训练中,为了训练球员快速抢断转身,教练在东西方向的足球场上画了一条直线,要求球员在这条直线上进行折返跑训练,如果约定向西为正,向东为负,将某球员的一组折返距练习记录如下(单位:米) :![]() ,
,![]() .
.
![]() 球员最后到达的地方在出发点的哪个方向?距出发点多远?
球员最后到达的地方在出发点的哪个方向?距出发点多远?
![]() 球员训练过程中,最远处离出发点 米?
球员训练过程中,最远处离出发点 米?
![]() 球员在这一组练习过程中,共跑了多少米?
球员在这一组练习过程中,共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图 ,AD 是∠BAC 的平分线,且 DF⊥AC 于 F,∠B=90°,DE=DC.

(1)求证:BE=CF.
(2)若△ADE 和△DCF 的面积分别是12和5,求△ABC 的面积.
(3)请你写出∠BAC与∠CDE有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOE=90°.
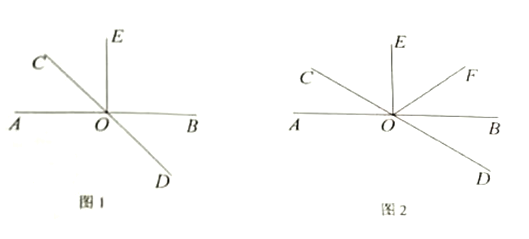
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对任意一个两位数![]() ,如果
,如果![]() 满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为
满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”,将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为![]() .例如:
.例如:![]() ,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以
,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为33÷11=3,所以![]() .根据以上定义,回答下列问题:
.根据以上定义,回答下列问题:
(1)填空:①下列两位数:40,42,44中,“迥异数”为_______;②计算:![]() =_______;
=_______;
(2)如果一个“迥异数”![]() 的十位数字是
的十位数字是![]() ,个位数字是
,个位数字是![]() ,且
,且![]() ,请求出“迥异数”
,请求出“迥异数”![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的20个小球,其中红球6个,黑球14个
(1)先从袋子中取出x(x>3)个红球后,再从袋子中随机摸出1个球,将“摸出黑球”,记为事件A.请完成下列表格.
事件A | 必然事件 | 随机事件 |
x的值 |
(2)先从袋子中取出m个红球,再放入2m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com