
【题目】已知:如图 ,AD 是∠BAC 的平分线,且 DF⊥AC 于 F,∠B=90°,DE=DC.

(1)求证:BE=CF.
(2)若△ADE 和△DCF 的面积分别是12和5,求△ABC 的面积.
(3)请你写出∠BAC与∠CDE有什么数量关系?并说明理由.
【答案】(1)详见解析;(2)39;(3)互补;
【解析】
(1)先由角平分线的性质就可以得出DB=DF,再证明△BDE≌△FDC就可以求出结论.(2)由△BDE和△FDC面积相等,△ABD和△ADF面积相等,转换得出△ABC的面积即可;(3)通过∠ACD=∠BED推出∠ACD+∠ AED=180°,再通过四边形AEDC的内角和为360°即可求出∠BAC与∠CDE的关系.
(1)证明:
∵∠B=90°,
∴BD⊥AB.
∵AD为∠BAC的平分线,且DF⊥AC,
∴DB=DF.
在Rt△BDE和Rt△FDC中,
![]()
∴Rt△BDE≌Rt△FDC(HL),
∴BE=CF
(2)解:∵△BDE≌△FDC
∴△ BDE的面积为5,
则S△ABD=17,
∵AD平分∠BAC,DB⊥AB,DF⊥AC,
∴S△ABD=S△ADF=17,
∴S△ABC=17+17+5=39
(3)解:∵△BDE≌△FDC
∴∠ACD=∠BED,
∵∠ BED+∠AED=180°,
∴∠ACD+∠AED=180°,
在四边形AEDC中,
∵四边形内角和为360°,∠ACD+∠AED=180°,
∴∠BAC +∠CDE=180°,即∠BAC 与∠CDE互补.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a,b,其中B,C,E在一条直线上,G在线段CD上,三角形AGE的面积为S.
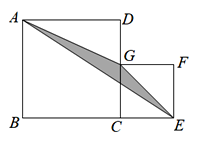
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a,b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是21,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.
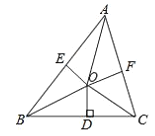
(1)试判断线段OD、OE、OF的大小关系.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(1,0),点B(0, ![]() ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
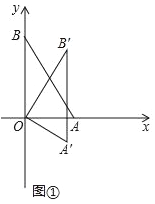
(Ⅰ)如图①,当α=30°时,求点B′的坐标;
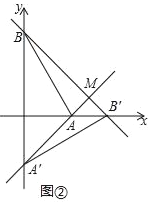
(Ⅱ)设直线AA′与直线BB′相交于点M.
如图②,当α=90°时,求点M的坐标;
②点C(﹣1,0),求线段CM长度的最小值.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)64的展开式中第三项的系数为( )
A. 2016 B. 2017 C. 2018 D. 2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com