Question

【题目】如图，已知△ABC的周长是21，BO、CO分别平分∠ABC和∠ACB，OD⊥BC于D，OE⊥AB，OF⊥AC，且OD=3．

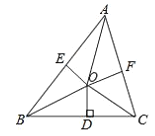
（1）试判断线段OD、OE、OF的大小关系．

（2）求△ABC的面积．

Answer 1

【答案】（1）OD=OE=OF，理由见解析；（2）31.5.

【解析】

（1）根据角平分线上的点到角两边的距离相等即可得出OD、OE、OF的大小关系；

（2）由S△ABC=S△BOC+ S△AOB+ S△AOC，利用三角形的面积公式进行求解即可.

解：（1）OD=OE=OF，理由如下：

∵BO平分∠ABC，OD⊥BC，OE⊥AB，

∴OD=OE，

∵CO平分∠ACB，OD⊥BC，OF⊥AC，

∴OD=OF，

∴OD=OE=OF；

（2）∵S△ABC=S△BOC+ S△AOB+ S△AOC，

S△BOC=，S△AOB=， S△AOC=，

∴S△ABC=++，

∵OD=OE=OF，

∴S△ABC=（BC+AB+AC），

∵AB+BC+AC=21，OD=3，

∴S△ABC==31.5.