练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

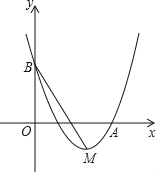
    【题目】如图在平面直角坐标系xOy中，O为坐标原点，二次函数y=x2+bx+c的图象经过点A（3，0）、点B（0，3），顶点为M．

    （1）求该二次函数的解析式；

    （2）求∠OBM的正切值．

    【答案】(1)y=x2﹣4x+3；（2）

    【解析】分析：（1）先把A、B两点的坐标代入y=x2+bx+c得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；

    （2）作MH⊥y轴于H，如图，先把抛物线解析式配成顶点式得到M点坐标，然后根据正切的定义求∠HBM的正切值即可．

    详解：（1）把A（3，0）、B（0，3）代入y=x2+bx+c得：，

    解得：，所以y=x2﹣4x+3；

    （2）作MH⊥y轴于H，如图，

    ∵y=x2﹣4x+3=（x﹣2）2﹣1，∴M（2，﹣1）．

    ∵MH⊥y轴，∴H（0，﹣1）．

    在Rt△BMH中，tan∠HBM==，即∠OBM的正切值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和，如23＝3＋5，33＝7＋9＋11，43＝13＋15＋17＋19，…，分裂后第一个数是____________（用含m的代数式表示）；若分裂后，其中有一个奇数是2019，则m的值是_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

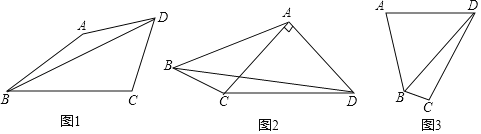
    【题目】已知：在四边形ABCD中，根据下列不同条件求BD长．

    （1）如图1，当∠ABC＝∠ADC＝30°，AD＝DC，AB＝9，BC＝12时，求BD的长．

    （2）如图2，当∠ABC＝∠ADC＝45°，AD⊥AC，AB＝6，BC＝5时，求BD的长．

    （3）如图3，当∠ABC＝2∠ADC＝120°，AD＝DC，四边形ABCD的面积为4时，请直接写出BD的长是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

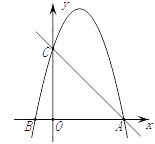
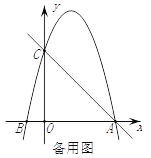
    【题目】如图，在平面直角坐标系中，已知点C(0，4)，点A、B在x轴上，并且OA＝OC＝4OB，动点P在过A、B、C三点的抛物线上．

    (1)求抛物线的函数表达式；

    (2)在直线AC上方的抛物线上，是否存在点P，使得△PAC的面积最大？若存在，求出P点坐标及ΔPAC面积的最大值；若不存在，请说明理由．

    (3)在x轴上是否存在点Q，使得△ACQ是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小方家住户型呈长方形，平面图如下(单位：米)，现准备铺设地面，三间卧室铺设木地板，其它区城铺设地砖.

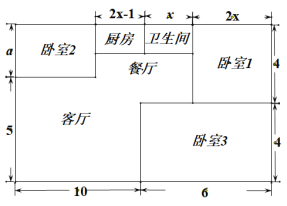
    (1)求a的值.

    (2)铺设地面需要木地板和地砖各多少平方米(用含的代数式表示)？

    (3)按市场价格，木地板单价为300元/平方米，地砖单价为100元/平方米，装修公司有两种活动方案，如表：

    活动方案

    木地板价格

    地砖价格

    总安装费

    A

    8折

    8.5折

    2000元

    B

    9折

    8.5折

    免收

    已知卧室2的面积是21平方米，则小方家应选择哪种活动，使铺设地面的总费用（包括材料费及安装费）更低？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

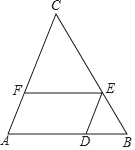
    【题目】如图，已知△ABC中，D、E、F分别是边AB、BC、CA上的点，且EF∥AB， =2．

    （1）设，．试用、表示；

    （2）如果△ABC的面积是9，求四边形ADEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【阅读理解】

    若， ， 为数轴上三点，若点到的距离是点到的距离的倍，我们就称点是的优点．例如，如图①，点表示的数为，点表示的数为．表示数的点到点的距离是，到点的距离是，那么点是的优点；又如，表示的点到点的距离是，到点的距离是，那么但点是的好点．

    【知识运用】

    如图②，、为数轴上两点，点所表示的数为，点所表示的数为．

    （）数__________所表示的点是的优点．

    （）如图③，， 为数轴上两点，点所表示的数为，点所表示的数为．现有一只电子蚂蚁从点出发，以个单位每秒的速度向左运动，到达点停止．当为何值时， 、和中恰有一个点为其余两点的好点？（请直接写出答案）

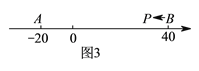
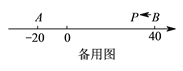
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，对角线AC、BD相交于点O，，，且∠ABC=900．

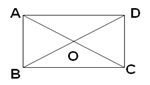
    （1）求证：四边形ABCD是矩形．

    （2）若∠ACB=300，AB=1，求①∠AOB的度数；②四边形ABCD的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ ACB=115O，BD=BC,AE=AC. 则∠ECD的度数为_________.

    查看答案和解析>>

    同步练习册答案