
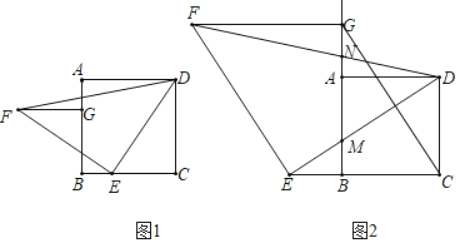
【题目】如图1,在正方形ABCD中,E是边BC上的点,将线段DE绕点E逆时针旋转90°得到EF,过点C作CG∥EF交BA(或其延长线)于点G,连接DF,FG.
(1)FG与CE的数量关系是 ,位置关系是 .
(2)如图2,若点E是CB延长线上的点,其它条件不变.
①(1)中的结论是否仍然成立?请作出判断,并给予证明;
②DE,DF分别交BG于点M,N,若BC=2BE,求![]() .
.
【答案】(1)FG=EC,FG∥EC.(2)①结论不变,见解析,②![]() =
=![]() .
.
【解析】
(1)结论:FG=EC,FG∥EC.证明四边形ECGF是平行四边形即可.
(2)①结论不变.证明四边形ECGF是平行四边形即可.
②如图2-1中,延长AG到H,使得AH=AD,连接DH,BD,在BC上截取一点K,使得BK=HN,连接MK,DK.首先证明MB=BK,设BC=a,MN=b,求出BM,BK,在Rt△BMK中,利用勾股定理即可解决问题.
解:(1)结论:FG=EC,FG∥EC.
理由:如图1中,
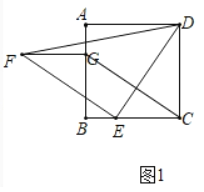
∵四边形ABCD是正方形,
∴BC=CD,∠CBG=∠DCE=90°,
∵∠DEF=90°,
∴∠FEB+∠DEC=90°,∠DEC+∠EDC=90°,
∴∠FEB=∠EDC,
∵CG∥EF,
∴∠GCB=∠FEB=∠EDC,
∴△GCB≌△EDC(ASA),
∴CG=DE,
∵EF=DE,
∴CG=EF,∵CG∥EF,
∴四边形ECGF是平行四边形,
∴FG=EC,FG∥EC.
(2)①结论不变.
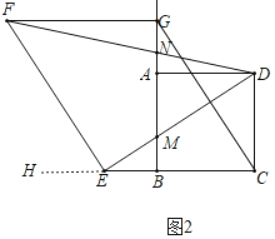
理由:延长CE到H.
∵四边形ABCD是正方形,
∴BC=CD,∠CBG=∠DCE=90°,
∵∠DEF=90°,
∴∠FEH+∠DEC=90°,∠DEC+∠EDC=90°,
∴∠FEH=∠EDC,
∵CG∥EF,
∴∠GCB=∠FEH=∠EDC,
∴△GCB≌△EDC(ASA),
∴CG=DE,
∵EF=DE,
∴CG=EF,∵CG∥EF,
∴四边形ECGF是平行四边形,
∴FG=EC,FG∥EC.
②如图2﹣1中,延长AG到H,使得AH=AD,连接DH,BD,在BC上截取一点K,使得BK=HN,连接MK,DK.
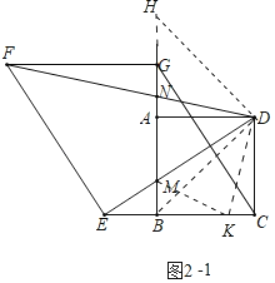
∵AH=AD=AB,DA⊥BH,
∴DH=DB,∠HDB=90°,
∵BK=HN,∠H=∠DBK=45°,
∴△NHD≌△KBD(SAS),
∴DN=DK,∠HDN=∠BDK,
∴∠HDB=∠NDK=90°,
∵∠MDN=45°,
∴∠NDM=∠KDM=45°,
∵DM=DM,
∴△NDM≌△KDM,
∴MN=MK,设BC=a,MN=b,
∵BC=2BE,
∴EB=![]() a,
a,
∵
∴![]() ,
,
∴BM=![]() a,
a,
∵BK=NH=2a﹣![]() a﹣b=
a﹣b=![]() a﹣b,
a﹣b,
在Rt△BMK中,∵MK2=BM2+BK2,
∴b2=(![]() a)2+(
a)2+(![]() a﹣b)2,
a﹣b)2,
整理得:![]() =
=![]() ,
,
∴![]() .
.
故答案为:(1)FG=EC,FG∥EC.(2)①结论不变,见解析,②![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,
OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的![]() ,那么点B′的坐标是【 】
,那么点B′的坐标是【 】

A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8厘米,BC=10厘米,点E在边AB上,且AE=2厘米,如果动点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,动点Q在线段CD上由C点向D点运动,设运动时间为t秒,当△BPE与△CQP全等时,t的值为( )

A. 2B. 1.5或2C. 2.5D. 2或2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
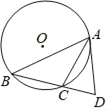
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:∠CAD=∠B.
(2)若AC是∠BAD的平分线,sinB=![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
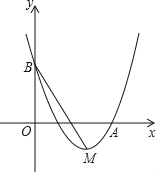
【题目】如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且弧CB=弧CD,CE⊥DA交DA的延长线于点E.
(1)求证:∠CAB=∠CAE;
(2)求证:CE是⊙O的切线;
(3)若AE=1,BD=4,求⊙O的半径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com