
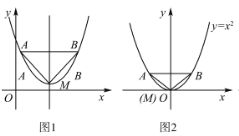
【题目】如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图2,则抛物线y=x![]() 的“完美三角形”斜边AB的长________.
的“完美三角形”斜边AB的长________.
科目:初中数学 来源: 题型:
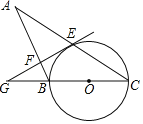
【题目】如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.
(1)求证:∠ABG=2∠C;
(2)若GF=3![]() ,GB=6,求⊙O的半径.
,GB=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励下岗工人再就业,某地市政府规定,企业按成本价提供产品给下岗人员自主销售,成本价与出厂价之间的差价由政府承担.老李按照政策投资销售本市生产的一种儿童面条.已知这种儿童面条的成本价为每袋12元,出厂价为每袋16元,每天销售量![]() (袋)与销售单价
(袋)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)老李在开始创业的第1天将销售单价定为17元,那么政府这一天为他承担的总差价为多少元?
(2)设老李获得的利润为![]() (元),当销售单价为多少元时,每天可获得最大利润?
(元),当销售单价为多少元时,每天可获得最大利润?
(3)物价部门规定,这种面条的销售单价不得高于24元,如果老李想要每天获得的利润不低于216元,那么政府每天为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
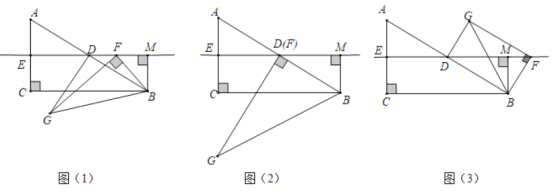
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 的垂线段
的垂线段![]() 垂足为
垂足为![]() .点
.点![]() 是直线
是直线![]() 上一动点,作
上一动点,作![]() 使
使![]() ,
,![]() 连接
连接![]() .
.
(1)观察猜想:如图(2),当点![]() 与点
与点![]() 重合时,则
重合时,则![]() 的值为 .
的值为 .
(2)问题探究:如图(1),当点![]() 与点
与点![]() 不重合时,请求出
不重合时,请求出![]() 的值及两直线
的值及两直线![]() 夹角锐角的度数,并说明理由
夹角锐角的度数,并说明理由
(3)问题解决:如图(3),当点![]() 在同一直线上时,请直接写出
在同一直线上时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中的三点A(1,0),B(-1,0),P(0,-1),将线段AB沿y轴向上平移m(m>0)个单位长度,得到线段CD,二次函数y=a(x-h)2+k的图象经过点P,C,D.
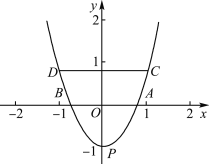
(1)当m=1时,a=______;当m=2时,a=______;
(2)猜想a与m的关系,并证明你的猜想;
(3)将线段AB沿y轴向上平移n(n>0)个单位长度,得到线段C1D1,点C1,D1分别与点A,B对应,二次函数y=2a(x-h)2+k的图象经过点P,C1,D1.
①求n与m之间的关系;
②当△COD1是直角三角形时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径.某校为了了解学生课外阅读情况,随机抽查了![]() 名学生,统计他们平均每天课外阅读时间
名学生,统计他们平均每天课外阅读时间![]() .根据
.根据![]() 的长短分为
的长短分为![]() ,
,![]() ,
,![]() ,
,![]() 四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图表中提供的信息,解答下面的问题:
四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图表中提供的信息,解答下面的问题:
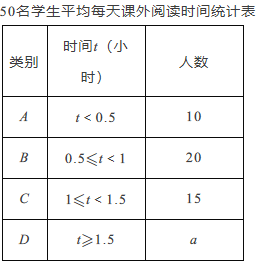
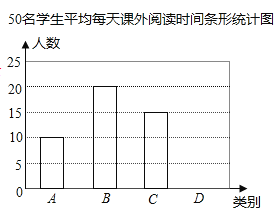
(1)本次调查的样本容量为_______;
(2)求表格中的![]() 的值,并在图中补全条形统计图(如图);
的值,并在图中补全条形统计图(如图);
(3)该校现有![]() 名学生,请你估计该校共有多少名学生的课外阅读时间不少于
名学生,请你估计该校共有多少名学生的课外阅读时间不少于![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
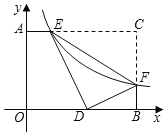
【题目】如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y![]() (k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为____.
(k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一个正三角形绕其中心最少旋转![]() ,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转 45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转______
,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转 45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转______![]() ,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为
,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为![]() ,则所得正八边形的面积为_______.
,则所得正八边形的面积为_______.


图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com