
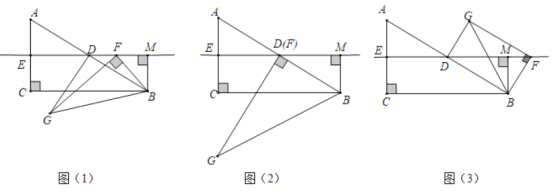
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 的垂线段
的垂线段![]() 垂足为
垂足为![]() .点
.点![]() 是直线
是直线![]() 上一动点,作
上一动点,作![]() 使
使![]() ,
,![]() 连接
连接![]() .
.
(1)观察猜想:如图(2),当点![]() 与点
与点![]() 重合时,则
重合时,则![]() 的值为 .
的值为 .
(2)问题探究:如图(1),当点![]() 与点
与点![]() 不重合时,请求出
不重合时,请求出![]() 的值及两直线
的值及两直线![]() 夹角锐角的度数,并说明理由
夹角锐角的度数,并说明理由
(3)问题解决:如图(3),当点![]() 在同一直线上时,请直接写出
在同一直线上时,请直接写出![]() 的值.
的值.
【答案】(1)2;(2)60°,见解析;(3)4+![]() 或4-
或4-![]()
【解析】
(1)由题意可知结论为当点F与点D重合时,则![]() 的值为2,并根据题意设BM=a,求出DM,GD即可解决问题;
的值为2,并根据题意设BM=a,求出DM,GD即可解决问题;
(2)由题意可知结论为![]() 的值为2,两直线GD、ED夹角锐角的度数为60°,并利用全等三角形的判定定理证明△BGD∽△BFM,可得结论;
的值为2,两直线GD、ED夹角锐角的度数为60°,并利用全等三角形的判定定理证明△BGD∽△BFM,可得结论;
(3)根据题意分两种情形:当点G在线段AF上时以及当点G在线段AF的延长线上时,分别进行求解即可.
解:(1) 设BM=a.
∵AE=EC,AD=DB,
∴DE∥BC,
∴∠BDM=∠ABC=30°,
∵BM⊥EM,
∴∠BMD=90°,
∴![]() ,
,
在Rt△GDB中,∵∠GDB=90°,∠G=30°,
∴![]() ,
,
∴![]() .
.
故答案为:2.
(2)在Rt△BDM中,设BM=a,则BD=2a,DM=![]() a
a
在Rt△BGF中,设BF=b,则BG=2b,FG=![]()
在△BGD与△BFM中,
∵BG:BF=2b:b=2a:a=BF:BM,∠DBG=60°-∠FBD=∠FBM
∴△BGD∽△BFM
则DG:FM=BD:BM=2a:a=2:1
即![]() 的值为2.
的值为2.
如图,延长GD、BF交于点P,
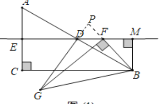
∵△BGD∽△BFM
∴∠PFD=∠MFB=∠BGD
则在△PDF与△PBG中,∠PDF=∠PBG=60°.
故![]() 的值为2,两直线GD、ED夹角锐角的度数为60°.
的值为2,两直线GD、ED夹角锐角的度数为60°.
(3)如图,有以下两种如图3①,图3②


如图3③,ED是△ABC的中垂线;
∵在Rt△AF1B和Rt△AF2B中,DA=DF1=DF2=DB
∴四边形AF2BF1是矩形
当点G在线段AF上时,在Rt△BF1G1中,
设BF1=x,则BG1=2x=AG1,F1G1=![]()
∴BG1:AF1=![]() :
:![]() =4-
=4-![]()
当点G在线段AF的延长线上时,在矩形AF2BF1中,
设AF2=BF1=x, F2B=AF1=![]()
∴BG2=2![]()
则BG2:AF2=2![]() :x=4+
:x=4+![]() .
.
∴![]() 的值为4+
的值为4+![]() 或4-
或4-![]() .
.


科目:初中数学 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
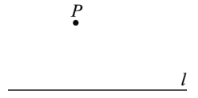
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,

①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:
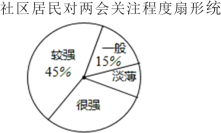
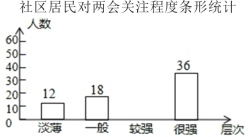
请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为![]() ,AD=2,则△ACO的面积为_________.
,AD=2,则△ACO的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图2,则抛物线y=x![]() 的“完美三角形”斜边AB的长________.
的“完美三角形”斜边AB的长________.
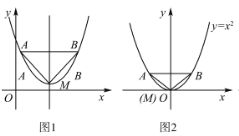
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】延迟开学期间,学校为了全面分析学生的网课学习情况,进行了一次抽样调查(把学习情况分为三个层次,![]() :能主动完成老师布置的作业并合理安排课外时间自主学习;
:能主动完成老师布置的作业并合理安排课外时间自主学习;![]() :只完成老师布置的作业;
:只完成老师布置的作业;![]() :不能完成老师布置的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
:不能完成老师布置的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:


(1)此次抽样调查中,共调查了__________名学生;
(2)将条形图补充完整;
(3)图2中![]() 所占的圆心角的度数为__________度;
所占的圆心角的度数为__________度;
(4)如果学校开学后对![]() 层次的学生进行奖励,根据抽样调查结果,请你估计该校1600名学生中大约有多少名学生能获得奖励?
层次的学生进行奖励,根据抽样调查结果,请你估计该校1600名学生中大约有多少名学生能获得奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
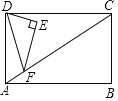
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com