
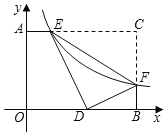
【题目】如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y![]() (k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为____.
(k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为____.
【答案】![]() .
.
【解析】
先证明Rt△MED∽Rt△BDF,则 ,而EM:DB=ED:DF=4:3,求出DB,在Rt△DBF中,利用勾股定理即可求解.
,而EM:DB=ED:DF=4:3,求出DB,在Rt△DBF中,利用勾股定理即可求解.
如图,过点E作EM⊥x轴于点M,
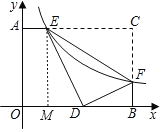
∵将△CEF沿EF对折后,C点恰好落在OB上的D点处,
∴∠EDF=∠C=90°,EC=ED,CF=DF,
∴∠MDE+∠FDB=90°,而EM⊥OB,
∴∠MDE+∠MED=90°,
∴∠MED=∠FDB,
∴Rt△MED∽Rt△BDF,
又∵EC=AC﹣AE=4![]() ,CF=BC﹣BF=3
,CF=BC﹣BF=3![]() ,
,
∴ED=4![]() ,DF=3
,DF=3![]() ,
,
∴ ,
,
∵EM:DB=ED:DF=4:3,而EM=3,
∴DB![]() ,
,
在Rt△DBF中,DF2=DB2+BF2,即(3![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得:k![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
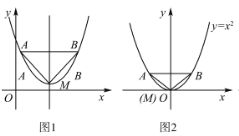
【题目】如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图2,则抛物线y=x![]() 的“完美三角形”斜边AB的长________.
的“完美三角形”斜边AB的长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】延迟开学期间,学校为了全面分析学生的网课学习情况,进行了一次抽样调查(把学习情况分为三个层次,![]() :能主动完成老师布置的作业并合理安排课外时间自主学习;
:能主动完成老师布置的作业并合理安排课外时间自主学习;![]() :只完成老师布置的作业;
:只完成老师布置的作业;![]() :不能完成老师布置的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
:不能完成老师布置的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:


(1)此次抽样调查中,共调查了__________名学生;
(2)将条形图补充完整;
(3)图2中![]() 所占的圆心角的度数为__________度;
所占的圆心角的度数为__________度;
(4)如果学校开学后对![]() 层次的学生进行奖励,根据抽样调查结果,请你估计该校1600名学生中大约有多少名学生能获得奖励?
层次的学生进行奖励,根据抽样调查结果,请你估计该校1600名学生中大约有多少名学生能获得奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】榴莲上市的时候,某水果行以“线上”与“线下”相结合的方式一共销售了![]() 箱榴莲.已知“线上”销售的每箱利润为
箱榴莲.已知“线上”销售的每箱利润为![]() 元.“线下”销售的每箱利润
元.“线下”销售的每箱利润![]() (元)与销售量
(元)与销售量![]() (箱)
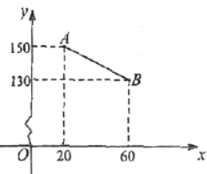
(箱)![]() 之间的函数关系如图中的线段
之间的函数关系如图中的线段![]() .
.
(1)求![]() 与
与![]() 之间的函数关系.
之间的函数关系.
(2)当“线下”的销售利润为![]() 元时,求
元时,求![]() 的值.
的值.
(3)实际“线下”销售时,每箱还要支出其它费用![]() 元
元![]() ,若“线上”与“线下”售完这
,若“线上”与“线下”售完这![]() 箱榴莲所获得的最大总利润为
箱榴莲所获得的最大总利润为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价.
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A、B两类图书共1000本 2.A类图书不少于600本 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
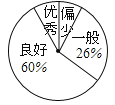
【题目】某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
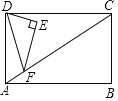
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
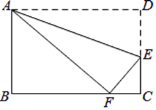
【题目】如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com