练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

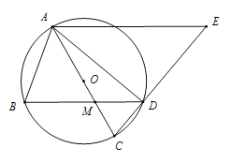
    【题目】如图，ABD内接于半径为5的⊙O，连结AO并延长交BD于点M，交圆⊙O于点C，过点A作AE//BD，交CD的延长线于点E,AB=AM.

    (1)求证：ABM∽ECA.

    (2)当CM=4OM时，求BM的长.

    (3)当CM=kOM时，设ADE的面积为, MCD的面积为，求的值(用含k的代数式表示).

    【答案】(1)证明见解析；(2);(3)

    【解析】

    （1）利用同弧所对的圆周角相等，以及平行线的性质得出角相等，再利用两角对应相等的两个三角形相似解题.

    （2）连接BC构造直角三角形，再过B作BF⊥AC，利用所得到的直角三角形，结合勾股定理解题.

    （3）过点M作出△MCD的高MG, 再由,得出线段间的比例关系，从而可得出结果.

    解：(1)∵弧CD=弧CD，

    ∴.

    ∵，

    ∴.

    ∴

    ∵弧AD=弧AD

    ∴

    ∴

    (2)连接BC，作，

    ∵半径为5，

    ∴.

    ∵，

    ∴，.

    ∴.

    由图可知AC为直径，,得.

    ，解得.

    在中，，则.

    ∴.

    在中，.

    (3)当，即，

    ，

    ，

    ∵，

    ∴，

    ∴.

    过M作,,(以AC为直径)，

    可知，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，双曲线经过的顶点和上的中点，轴，点的坐标为．则（1）点的坐标为______．（2）的面积是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着互联网的高速发展，人们的支付方式发生了巨大改变，某学习小组抽样调查了春节期间某商场顾客的支付方式，主要有现金支付、银联卡支付和手机支付，调查得知使用这三种支付的人数比为，手机支付已成为市民购物便捷支付方式．手机支付主要有以下三种方式：~支付宝，~微信，~其他．现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图．

    （1）扇形统计图中，________；请补全条形统计图；

    （2）若该商场春节期间共20000人购物，请估计用支付宝进行支付的人数．

    （3）经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元，求这天顾客每笔交易的平均金额．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

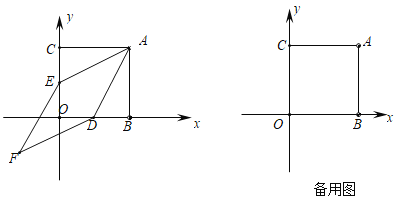
    【题目】如图，在平面直角坐标系中，正方形ABOC的两直角边分别在坐标轴的正半轴上，分别过OB，OC的中点D，E作AE，AD的平行线，相交于点F， 已知OB=8．

    （1）求证：四边形AEFD为菱形．

    （2）求四边形AEFD的面积．

    （3）若点P在x轴正半轴上(异于点D)，点Q在y轴上，平面内是否存在点G，使得以点A，P， Q，G为顶点的四边形与四边形AEFD相似？若存在，求点P的坐标；若不存在，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在正方形ABCD中，对角线AC与BD相交于点O，AE，DF分别是∠OAD与∠ODC的平分线，AE的延长线与DF相交于点G，则下列结论：①AG⊥DF；②EF∥AB；③AB＝AF；④AB＝2EF．其中正确的结论是（　　）

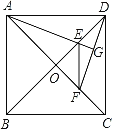
    A.①②B.③④C.①②③D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知E、F分别是ABCD的边BC，AD上的点，且BE＝DF．

    （1）求证：四边形AECF是平行四边形；

    （2）若四边形AECF是菱形，且BC＝8，∠BAC＝90°，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

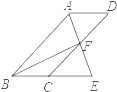
    【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

    （1）求证：BE=CD；

    （2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

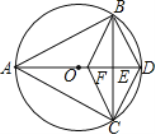
    【题目】如图，已知△ABC内接于⊙O，且AB＝AC，直径AD交BC于点E，F是OE上的一点，CFBD．

    （1）求证：BE＝CE；

    （2）试判断四边形BFCD的形状，并说明理由；

    （3）若BC＝6，AD＝10，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是半圆的直径，P是半圆与直径AB所围成的图形的外部的一定点，D是直径AB上一动点，连接PD并延长,交半圆于点C,连接AC,BC．已知AB=6 cm，设A，D两点之间的距离为x cm，A，C两点之间的距离为y1 cm，B，C两点之间的距离为y2 cm．

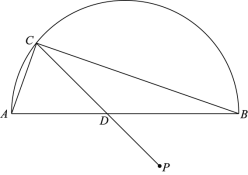
    小明根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．

    下面是小明的探究过程，请补充完整：

    （1）按照下表自变量x的值进行取点、画图、测量，分别得到y1，y2与x的几组对应值；

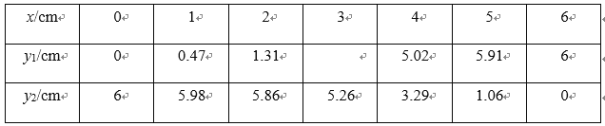
    （2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），

    （x， y2），并画出函数y1，y2的图象；

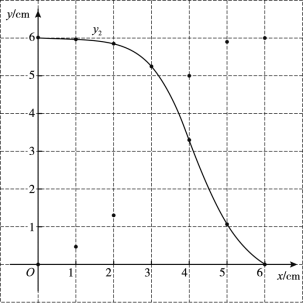
    （3）结合函数图象，解决问题：当△ABC有一个角的正弦值为时，AD的长约为________cm．

    查看答案和解析>>

    同步练习册答案