
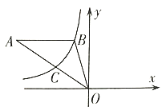
【题目】如图,双曲线![]()
![]() 经过
经过![]() 的顶点
的顶点![]() 和
和![]() 上的中点
上的中点![]() ,
,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() .则(1)点
.则(1)点![]() 的坐标为______.(2)
的坐标为______.(2)![]() 的面积是_______.
的面积是_______.
【答案】![]()
![]()
【解析】
(1)由AB∥x轴,点B的坐标为(-1,4),可设A(x,4),由OA边上的中点是C,可得点C的坐标为(![]() x,2),根据双曲线y=
x,2),根据双曲线y=![]() (x<0)经过点B和点C,列出方程求出x的值即可;
(x<0)经过点B和点C,列出方程求出x的值即可;
(2)根据A、B两点的坐标求出AB的长以及AB边上的高,根据三角形面积公式即可求出三角形OAB的面积.
解:(1)∵AB∥x轴,点B的坐标为(-1,4),
∴可设A(x,4),
∵OA边上的中点是C,
∴点C的坐标为(![]() x,2),
x,2),
∵双曲线y=![]() (x<0)经过点B和点C,
(x<0)经过点B和点C,
∴![]() x×2=-1×4,
x×2=-1×4,
∴x=-4,
∴点C的坐标为(-2,2),
故答案为:(-2,2);
(2)∵A(-4,4),B(-1,4),
∴AB=-1-(-4)=3,AB边上的高为4,
∴△OAB的面积是:![]() ×3×4=6.
×3×4=6.
故答案为:6.


科目:初中数学 来源: 题型:
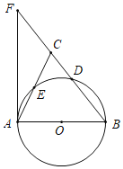
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E时![]() 的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=10.tan∠FAC=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售某种品牌的空调和电风扇:
(1)已知购进8台空调和20台电风扇共需17400元,购进10台空调和30台电风扇共需22500元,求每台空调和电风扇的进货价;
(2)已知空调标价为2500元/台,电风扇标价为250元/台.若商场购进空调和电风扇共60台,并全部打八折出售,设其中空调的数量为a台,商场通过销售这批空调和电风扇获得的利润为w元,求w和a之间的函数关系式;
(3)在(2)的条件下,若这批空调和电风扇的进货价不超过45300元,商场通过销售这批空调和电风扇获得的利润又不低于6000元,问商场共有多少种不同的进货方案,哪种进货方案获得的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
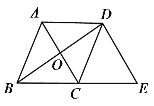
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,AB=5,AC=6,AC的平行线DE交BC的延长线于点E,则四边形ACED的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,![]() 月
月![]() 日是母亲节,浩浩去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支
日是母亲节,浩浩去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支![]() 元,兰花每支
元,兰花每支![]() 元,浩浩只有
元,浩浩只有![]() 元,还想留着
元,还想留着![]() 元购买卡片.希望购买花的支数为
元购买卡片.希望购买花的支数为![]() 支,其中至少有一支是兰花.浩浩一共有多少种可能的购买方案?列出所有方案.
支,其中至少有一支是兰花.浩浩一共有多少种可能的购买方案?列出所有方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 上的任一点,过点
上的任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于
于![]() .
.
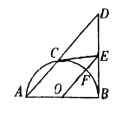
(1)求证:![]() ;
;
(2)填空:①当![]() _____时,四边形
_____时,四边形![]() 是正方形;
是正方形;
②当![]() _____时,四边形
_____时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )

A.8.5B.15C.17D.34
查看答案和解析>>
科目:初中数学 来源: 题型:
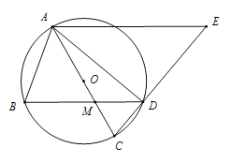
【题目】如图,ABD内接于半径为5的⊙O,连结AO并延长交BD于点M,交圆⊙O于点C,过点A作AE//BD,交CD的延长线于点E,AB=AM.
(1)求证:ABM∽ECA.
(2)当CM=4OM时,求BM的长.
(3)当CM=kOM时,设ADE的面积为![]() , MCD的面积为
, MCD的面积为![]() ,求
,求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com