
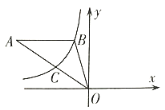
【题目】如图,双曲线![]()
![]() 经过
经过![]() 的顶点
的顶点![]() 和
和![]() 上的中点
上的中点![]() ,
,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() .则(1)点
.则(1)点![]() 的坐标为______.(2)
的坐标为______.(2)![]() 的面积是_______.
的面积是_______.
【答案】![]()
![]()
【解析】
(1)由AB∥x轴,点B的坐标为(-1,4),可设A(x,4),由OA边上的中点是C,可得点C的坐标为(![]() x,2),根据双曲线y=
x,2),根据双曲线y=![]() (x<0)经过点B和点C,列出方程求出x的值即可;
(x<0)经过点B和点C,列出方程求出x的值即可;
(2)根据A、B两点的坐标求出AB的长以及AB边上的高,根据三角形面积公式即可求出三角形OAB的面积.
解:(1)∵AB∥x轴,点B的坐标为(-1,4),
∴可设A(x,4),
∵OA边上的中点是C,
∴点C的坐标为(![]() x,2),
x,2),
∵双曲线y=![]() (x<0)经过点B和点C,
(x<0)经过点B和点C,
∴![]() x×2=-1×4,
x×2=-1×4,
∴x=-4,
∴点C的坐标为(-2,2),
故答案为:(-2,2);
(2)∵A(-4,4),B(-1,4),
∴AB=-1-(-4)=3,AB边上的高为4,
∴△OAB的面积是:![]() ×3×4=6.
×3×4=6.
故答案为:6.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售![]() 两种型号的口罩,已知销售
两种型号的口罩,已知销售![]() 只
只![]() 型和
型和![]() 只
只![]() 型的利润为
型的利润为![]() 元,销售
元,销售![]() 只
只![]() 型和
型和![]() 只
只![]() 型的利润为
型的利润为![]() 元.
元.
(1)求每只![]() 型口罩和
型口罩和![]() 型口罩的销售利润;
型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共![]() 只,其中
只,其中![]() 型口罩的进货量不超过
型口罩的进货量不超过![]() 型口罩的
型口罩的![]() 倍,设购进
倍,设购进![]() 型口罩
型口罩![]() 只,这
只,这![]() 只口罩的销售总利润为
只口罩的销售总利润为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②该药店购进![]() 型、
型、![]() 型口罩各多少只,才能使销售总利润最大?
型口罩各多少只,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边长在上方作正方形
为边长在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 交于点
交于点![]()
![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
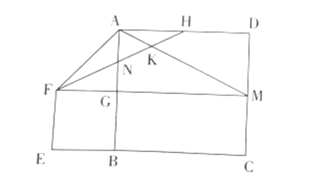
A.①②B.①④C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
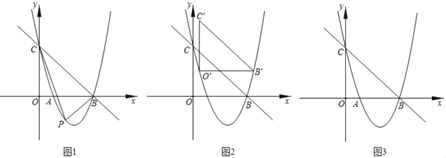
【题目】如图1,抛物线y=ax2﹣![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() x+3经过点B,C.
x+3经过点B,C.
(1)求抛物线的解析式;
(2)若点P为直线BC下方的抛物线上一动点(不与点B,C重合),则△PBC的面积能够等于△BOC的面积吗?若能,求出相应的点P的坐标;若不能,请说明理由;
(3)如图2,现把△BOC平移至如图所示的位置,此时三角形水平方向一边的两个端点点O′与点B′都在抛物线上,称点O′和点B′为△BOC在抛物线上的一“卡点对”;如果把△BOC旋转一定角度,使得其余边位于水平方向然后平移,能够得到这个三角形在抛物线上新的“卡点对”.请直接写出△BOC在已知抛物线上所有“卡点对”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.

(1)求反比例函数和一次函数的解析式;
(2)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com