
【题目】商场销售某种品牌的空调和电风扇:
(1)已知购进8台空调和20台电风扇共需17400元,购进10台空调和30台电风扇共需22500元,求每台空调和电风扇的进货价;
(2)已知空调标价为2500元/台,电风扇标价为250元/台.若商场购进空调和电风扇共60台,并全部打八折出售,设其中空调的数量为a台,商场通过销售这批空调和电风扇获得的利润为w元,求w和a之间的函数关系式;
(3)在(2)的条件下,若这批空调和电风扇的进货价不超过45300元,商场通过销售这批空调和电风扇获得的利润又不低于6000元,问商场共有多少种不同的进货方案,哪种进货方案获得的利润最高?最高利润是多少?
【答案】(1)1800元;150元;(2)![]() ;(3)三种方案:方案一:空调20台,电风扇40台;方案二:空调21台,电风扇39台;方案三:空调22台,电风扇38台;当进货空调22台,电风扇38台时,利润最高,最高利润为6300元
;(3)三种方案:方案一:空调20台,电风扇40台;方案二:空调21台,电风扇39台;方案三:空调22台,电风扇38台;当进货空调22台,电风扇38台时,利润最高,最高利润为6300元
【解析】
(1)设每台空调、电风扇的进货价分别为x,y元,根据题意得出等量关系,列出方程组解之即可;
(2)根据题意,分别表示出空调和电风扇的价格,利用利润=售价-进价得到利润w和台数a的函数关系式;
(3)利用这批空调和电风扇的进货价不超过45300元,商场通过销售这批空调和电风扇获得的利润又不低于6000元,组成不等式组求出,即可得到结论.
(1)设每台空调、电风扇的进货价分别为x,y元,根据题意得:
![]() ,
,
解得:![]() ,
,
答:每台空调进货价为1800元,每台电风扇进货价为150元;
(2)根据题意得:
![]()
=![]()
所以w与a之间的函数关系式为![]()
(3)由题意得:
![]() ,
,
解得:20≤a≤22,
∵a为整数,
∴a=20或21或22,
∵a﹥0
∴w随a的增大而增大,
∴当a=22时,w最大,最大值为6300元.
∴有三种方案:
方案一:空调20台,电风扇40台;
方案二:空调21台,电风扇39台;
方案三:空调22台,电风扇38台;
当进货空调22台,电风扇38台时,利润最高,最高利润为6300元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,以
,以![]() 为边在第一象限内作正方形
为边在第一象限内作正方形![]() ,且双曲线
,且双曲线![]() 经过点
经过点![]() .
.
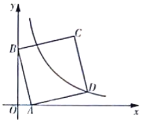
(1)求![]() 的值;
的值;
(2)将正方形![]() 沿
沿![]() 轴负方向平移得到正方形
轴负方向平移得到正方形![]() ,当点
,当点![]() 恰好落在双曲线
恰好落在双曲线![]() 上时,求
上时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
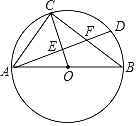
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,与抛物线
,与抛物线![]() 交于点
交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是线段
是线段![]() 上(不与
上(不与![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作矩形
为边作矩形![]() ,请求出矩形
,请求出矩形![]() 周长的最大值;
周长的最大值;
(3)若点![]() 在
在![]() 轴正半轴上,当
轴正半轴上,当![]() 恰好是等腰三角形时,请直接写出点
恰好是等腰三角形时,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com