
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,以
,以![]() 为边在第一象限内作正方形
为边在第一象限内作正方形![]() ,且双曲线
,且双曲线![]() 经过点
经过点![]() .
.
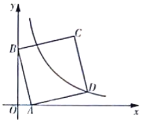
(1)求![]() 的值;
的值;
(2)将正方形![]() 沿
沿![]() 轴负方向平移得到正方形
轴负方向平移得到正方形![]() ,当点
,当点![]() 恰好落在双曲线
恰好落在双曲线![]() 上时,求
上时,求![]() 的面积.
的面积.
【答案】(1)5;(2)6.
【解析】
(1)过点D作DE⊥x轴于点E,根据正方形的性质以及角的计算即可证出△OBA≌△EAD(AAS),结合点A、B的坐标即可得出点D的坐标,由点B的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数解析式;
(2)再根据正方形的性质以及点A、B、D的坐标即可得出点C的坐标,由平移可知C与![]() 的纵坐标相同,可求得
的纵坐标相同,可求得![]() 的坐标,从而得到
的坐标,从而得到![]() 的长,即可求出
的长,即可求出![]() 的面积.
的面积.
(1)过点D作DE⊥x轴于点E,如图所示,
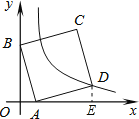
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=AD,
∴∠OAB+∠EAD=90°,
又∵∠OAB+∠OBA=90°,
∴∠OBA=∠EAD,
在△OBA和△EAD中,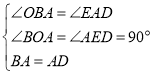 ,
,
∴△OBA≌△EAD(AAS),
∴BO=AE,OA=ED.
∵A(1,0),
∴AO=1,
∵![]() ,
,
∴![]() ,
,
∴AE=BO=4,ED=OA=1,
∴D(5,1),
将D代入![]() ,
,
![]() ,即
,即![]() ;
;
(2)∵A(1,0),B(0,4),且四边形ABCD为正方形,
∴C(4,5),
由![]() 可知
可知![]() ,
,
由平移可知C与![]() 的纵坐标相同,
的纵坐标相同,
在![]() 上,当
上,当![]() 时,
时,![]() ,
,
∴![]() (1,5),
(1,5),![]() ,
,
∵D(5,1),C(4,5),![]() (1,5),
(1,5),
∴D到![]() 的距离为5-1=4,
的距离为5-1=4,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=4,点P在![]() 上运动(点P不与点A、B重合),且∠APB=30°,设图中阴影部分的面积为y.
上运动(点P不与点A、B重合),且∠APB=30°,设图中阴影部分的面积为y.
(1)⊙O的半径为 ;
(2)若点P到直线AB的距离为x,求y关于x的函数表达式,并直接写出自变量x的取值范围.
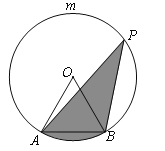
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选好志愿者,支持军运会.武汉市某校团委组织了一次八年级600名学生参加的“武汉军运知多少”知识大赛.为了了解本次大赛的成绩,随机抽取了部分学生的成绩作为样本,按A,B,C,D四个等级进行统计,制成如下不完整的统计图.(说明:A级80分- 100分,B级70分-79分,C级60-69分,D级0分-59分)
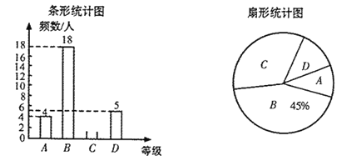
根据所给信息,解答以下问题:
(1)在扇形统计图中,C级对应的扇形的圆心角是_______度;
(2)直接写出条形统计图B级的頻数_______;
(3)所抽取学生的足球运球测试成绩的中位数会落在_______等级;
(4)若成绩达到A级的学生可以选为志愿者,请估计该校八年级600名学生中可以选为志愿者学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
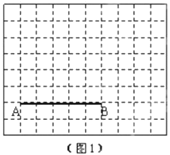
【题目】图1、图2分别是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段![]() 的两个端点均在小正方形的顶点上.
的两个端点均在小正方形的顶点上.
(1)在图1中画出以![]() 为直角边的直角
为直角边的直角![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() ;
;
(2)在图2中画出以![]() 为腰的钝角等腰
为腰的钝角等腰![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() 的面积为10.并直接写出线段
的面积为10.并直接写出线段![]() 的长.
的长.
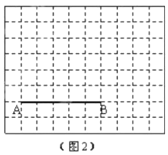
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B分别在反比例函数![]() (x>0),
(x>0),![]() (k<0,x>0)的图象上.点B的横坐标为4,且点B在直线y=x﹣5上.
(k<0,x>0)的图象上.点B的横坐标为4,且点B在直线y=x﹣5上.
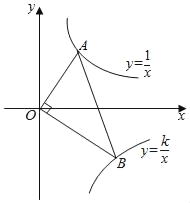
(1)求k的值;(2)若OA⊥OB,求tan∠ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com