
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 上的任一点,过点
上的任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于
于![]() .
.
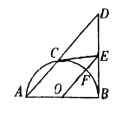
(1)求证:![]() ;
;
(2)填空:①当![]() _____时,四边形
_____时,四边形![]() 是正方形;
是正方形;
②当![]() _____时,四边形
_____时,四边形![]() 是菱形.
是菱形.
【答案】(1)见解析;(2)①![]() ,②
,②![]()
【解析】
(1)连接BC,由AB为圆的直径,可得![]() ,CE为⊙O的切线,DB⊥AB,可得EC=EB,可得
,CE为⊙O的切线,DB⊥AB,可得EC=EB,可得![]() ,再利用等角的余角相等得到
,再利用等角的余角相等得到![]() ,因此CE=ED,
,因此CE=ED,
(2)①利用四边形OCEB是正方形,得∠CED=90°,结合CE=ED,利用等腰直角三角形的性质可得答案; ②利用四边形OACF是菱形,得△OAC为等边三角形,利用DB⊥AB,直角三角形两锐角互余可得到答案.
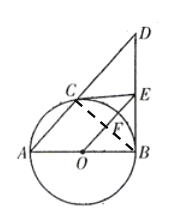
(1)证明:如图,连接![]() ,
,
 ,
,
![]() 为
为![]() 的直径,
的直径,![]()
![]() ,
,![]()
![]() 为
为![]() 切线,
切线,![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
![]()
(2)①如图,

若四边形OCEB是正方形, 则∠CEB=90°,
<> ∴∠CED=90°,∵CE=ED, ∴∠D=∠DCE=45°,
故答案为45°;
②若四边形OACF是菱形,
则OA=AC, ∵OA=OC,
∴△OAC为等边三角形,
∴∠A=60°,
∵DB⊥AB, ∴∠A+∠D=90°,
∴∠D=90°-60°=30°,
故答案为30°.


科目:初中数学 来源: 题型:
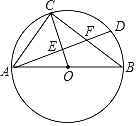
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
<>

请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
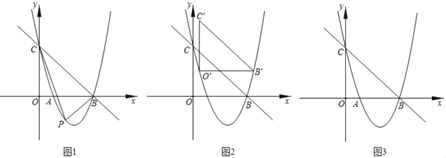
【题目】如图1,抛物线y=ax2﹣![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() x+3经过点B,C.
x+3经过点B,C.
(1)求抛物线的解析式;
(2)若点P为直线BC下方的抛物线上一动点(不与点B,C重合),则△PBC的面积能够等于△BOC的面积吗?若能,求出相应的点P的坐标;若不能,请说明理由;
(3)如图2,现把△BOC平移至如图所示的位置,此时三角形水平方向一边的两个端点点O′与点B′都在抛物线上,称点O′和点B′为△BOC在抛物线上的一“卡点对”;如果把△BOC旋转一定角度,使得其余边位于水平方向然后平移,能够得到这个三角形在抛物线上新的“卡点对”.请直接写出△BOC在已知抛物线上所有“卡点对”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点P是平行四边形ABCD外一点,PE∥AB交BC于点E.PA、PD分别交BC于点M、N,点M是BE的中点.
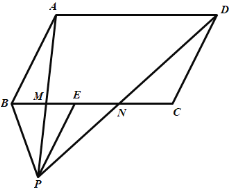
(1)求证:CN=EN;
(2)若平行四边形ABCD的面积为12,求△PMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
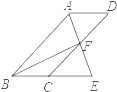
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com