
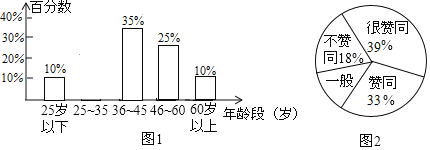
【题目】某城市响应“绿水青山就是金山银山”的号召,准备在全市宣传开展“垃圾分类”活动,先对随机抽取的![]() 名公民的年龄段分布情况和对“垃圾分类”所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
名公民的年龄段分布情况和对“垃圾分类”所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)补全条形图;
(2)扇形图中态度为“一般”所对应的扇形的圆心角的度数是 ;
(3)这次随机调查中,年龄段是“![]() 岁一下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ;
岁一下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,这个城市总人口大约![]() 万人,则对开展“垃圾分类”持“支持”态度的估计有多少万人?
万人,则对开展“垃圾分类”持“支持”态度的估计有多少万人?
【答案】(1)详见解析;(2)36°;(3)![]() ;(4)
;(4)![]() 万人.
万人.
【解析】
(1)用整体“1”减去已知年龄段所占的百分比,得出25~35岁所占的百分比即可补全条形统计图;
(2)先求出态度为“一般”所占的百分比,再用所得结果乘以360°即可求出结果;
(3)求出25岁以下的人数,用“不赞成”的人数除以25岁以下的人数,即可得解;
(4)用样本估计总体即可求出结果.
(1)25~35岁所占百分比为:1-10%-35%-25%-10%=20%,
故条形图如下:
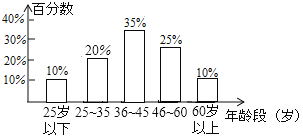
(2)态度为“一般”的所占百分比为:1-18%-39%-33%=10%,
∴态度为“一般”所对应的扇形的圆心角的度数是:360°×10%=36°;
(3)1000×10%=100(人)
∴“不赞成”的占的百分比为:
![]()
(4)![]() (万人)
(万人)


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】某市在九年级“线上教学”结束后,为了了解学生的视力情况,抽查了部分学生进行视力检查.根据检查结果,制作下面不完整的统计图表.

(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果势视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数,根据上述图表信息,你对视力保护有什么建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,![]() ,
,![]() 于点D,
于点D,![]() 于点E,交AD于点F,点M是BC的中点,连接FM并延长交AB的垂线BH于点H.下列说法中错误的是( )
于点E,交AD于点F,点M是BC的中点,连接FM并延长交AB的垂线BH于点H.下列说法中错误的是( )
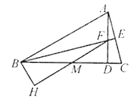
A.若![]() ,则
,则![]()
B.若![]() ,则
,则![]()
C.若![]() (点M与点D重合),则
(点M与点D重合),则![]()
D.若![]() (点B与点D重合),则
(点B与点D重合),则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
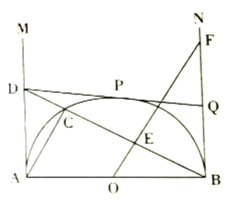
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,射线
,射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆
交半圆![]() 于点
于点![]() ,连接
,连接![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过点
.过点![]() 作半圆的切线
作半圆的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,口罩供不应求.某口罩企业为指导生产,在二月份期间对甲乙丙丁四条生产线日产量进行调研,根据调研数据,绘制出如下两幅不完整的统计图.观察统计图,请解答以下问题:
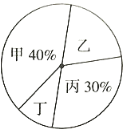
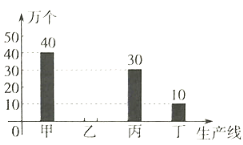
(1)求二月份该企业口罩单日产量(二月份计![]() 天).
天).
(2)求乙条生产线单日产量是多少,并补全频数分布直方图.
(3)为满足市场需求,该公司改进生产技术,使得口罩产量在二月的基础上逐月提高,已知![]() 月份口罩产量为
月份口罩产量为![]() 万只,若三月份和四月份口罩月产量平均增长率相同,求每月的平均增长率.
万只,若三月份和四月份口罩月产量平均增长率相同,求每月的平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 问题发现:如图![]() , 在
, 在![]() 中,
中,![]() ,
,![]() , 点
, 点![]() 是
是![]() 的中点, 以点
的中点, 以点![]() 为顶点作正方形
为顶点作正方形![]() , 使点
, 使点![]() ,
,![]() 分别在
分别在![]() 和DF上, 连接
和DF上, 连接![]() ,
,![]() ,则线段
,则线段![]() 和
和![]() 数量关系是 .
数量关系是 .
(2) 类比探究:如图![]() , 保持
, 保持![]() 固定不动, 将正方形
固定不动, 将正方形![]() 绕点
绕点![]() 旋转
旋转![]() ,则
,则![]() 中的结论是否成立?如果成立,请证明;如果不成立,请说明理由
中的结论是否成立?如果成立,请证明;如果不成立,请说明理由
(3)解决问题:若![]() ,在
,在![]() 的旋转过程中,连接
的旋转过程中,连接![]() ,请直接写出
,请直接写出![]() 的最大值
的最大值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水产养殖户开发一个三角形状的养殖区域,A、B、C三点的位置如图所示.已知∠CAB=105°,∠B=45°,AB=100![]() 米.(参考数据:
米.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)
≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)

(1)求养殖区域△ABC的面积;
(2)养殖户计划在边BC上选一点D,修建垂钓栈道AD,测得∠CAD=40°,求垂钓栈道AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以3元/本的价格购进某种笔记本若干,然后以5元/本的价格出售,每天售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若每本降价![]() 元,则每天的销售量是________本(用含
元,则每天的销售量是________本(用含![]() 的代数式表示).
的代数式表示).
(2)要想每天赢利60元,该超市需将每本的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com