
【题目】△ABC中,AB=AC,∠ABC=α,过点A作直线MN,使MN∥BC,点D在直线MN上,作射线BD,将射线BD绕点B顺时针旋转角α后交直线AC于点E.
(1)如图①,当α=60°,且点D在射线AN上时,直接写出线段AB,AD,AE的数量关系.
(2)如图②,当α=45°,且点D在射线AN上时,直写出线段AB、AD、AE的数量关系,并说明理由.
(3)当α=30°时,若点D在射线AM上,∠ABE=15°,AD=![]() ﹣1,请直接写出线段AE的长度.
﹣1,请直接写出线段AE的长度.

【答案】(1)AE=AB+AD;(2)AE=AB+![]() AD,见解析;(3)线段AE的长度为
AD,见解析;(3)线段AE的长度为![]() ﹣1或2﹣
﹣1或2﹣![]()
【解析】
(1)当α=60°时,可得△ABC是等边三角形,判定△BAD≌△BCE,即可得到AD=CE,进而得到AE=AC+CE=AB+AD;
(2)当α=45°时,可得△ABC是等腰直角三角形,判定△BAD∽△BCE,可得CE=![]() AD,进而得出AE=AC+CE=AB+
AD,进而得出AE=AC+CE=AB+![]() AD;
AD;
(3)分两种情况:点E在线段AC上,点E在CA的延长线上,分别画出图形,依据∠ABE=15°,AD=![]() ﹣1,即可得到线段AE的长度.
﹣1,即可得到线段AE的长度.
(1)∵当α=60°时,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
又∵AB=AC,
∴△ABC是等边三角形,
∴AB=CB,∠ACB=60°,
∴∠BCE=120°,
∵MN∥BC,
∴∠BAD=180°﹣∠ABC=120°,
∴∠BAD=∠BCE,
∴△BAD≌△BCE,
∴AD=CE,
∴AE=AC+CE=AB+AD;
(2)AE=AB+![]() AD.
AD.
理由:当α=45°时,∠ABC=∠DBE=45°,
∴∠ABD=∠CBE,
∵AB=AC,
∴∠ABC=∠ACB=45°,∠BAC=90°,
∴△ABC是等腰直角三角形,
∴BC=![]() AB,
AB,
∵MN∥BC,
∴∠BAD=180°﹣∠ABC=135°,
∵∠BCE=180°﹣∠ACB=135°,
∴∠BAD=∠BCE,
∴△BAD∽△BCE,
∴![]() =
=![]() =
=![]() ,
,
∴CE=![]() AD,
AD,
∴AE=AC+CE=AB+![]() AD;
AD;
(3)线段AE的长度为![]() ﹣1或2﹣
﹣1或2﹣![]() .
.
由题可得,∠ABC=∠DBE=∠BAD=30°,
分两种情况:
①如图所示,当点E在线段AC上时,

∵∠ABE=15°=![]() ∠ABC=
∠ABC=![]() ∠DBE,
∠DBE,
∴∠ABD=∠ABE=15°,
在BE上截取BF=BD,易得△ABD≌△ABF,
∴AD=AF=![]() ﹣1,∠ABC=∠BAD=∠BAF=30°,
﹣1,∠ABC=∠BAD=∠BAF=30°,
∴∠AFE=∠ABF+∠BAF=15°+30°=45°,
又∵∠AEF=∠CBE+∠C=15°+30°=45°,
∴∠AFE=∠AEF,
∴AE=AF=![]() ﹣1;
﹣1;
②如图所示,当点E在CA的延长线上时,

过D作DF⊥AB于F,过E作EG⊥BC于G,
∵AD=![]() ﹣1,∠DAF=30°,
﹣1,∠DAF=30°,
∴DF=![]() ,AF=
,AF=![]() ,
,
∵∠DBF=15°+30°=45°,
∴∠DBF=∠BDF,
∴BF=DF=![]() ,AB=
,AB=![]() +
+![]() =1=AC,
=1=AC,
易得△ABC中,BC=![]() ,
,
∵∠EBG=15°+30°=45°,
∴∠BEG=∠EBG,
设BG=EG=x,则CG=![]() ﹣x,
﹣x,
∵Rt△CEG中,tanC=![]() ,即
,即![]() =
=![]() ,
,
∴x=![]() =EG,
=EG,
∴CE=2EG=3﹣![]() ,
,
∴AE=CE﹣AC=3﹣![]() ﹣1=2﹣
﹣1=2﹣![]()
综上所述所,线段AE的长度为![]() ﹣1或2﹣
﹣1或2﹣![]() .
.


科目:初中数学 来源: 题型:
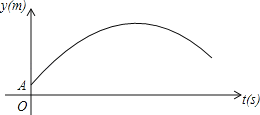
【题目】如图,某足球运动员站在点O处练习射门.将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,己知足球飞行0.8s时,离地面的高度为3.5m.
(1)a= ,c= ;
(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?
(3)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
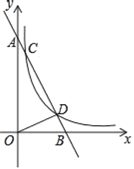
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,直线AB与反比例函数y=![]() (m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)分别求m、n的值;
(2)连接OD,求△ADO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 购买江苏省体育彩票有“中奖”与“不中奖”两种情况,所以中奖的概率是![]()
B. 国家级射击运动员射靶一次,正中靶心是必然事件
C. 如果在若干次试验中一个事件发生的频率是![]() ,那么这个事件发生的概率一定也是
,那么这个事件发生的概率一定也是![]()
D. 如果车间生产的零件不合格的概率为![]() ,那么平均每检查1000个零件会查到1个次品
,那么平均每检查1000个零件会查到1个次品
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发城在冬天到来之际进了一批保暖衣,男生的保暖衣每件价格60元,女生的保暖衣每件价格40元,第一批共购买100件.
(1)第一批购买的保暖衣的总费用不超过5400元,求女生保暖衣最少购买多少件?
(2)第二批购买保暖衣,购买男、女生保暖衣的件数比为![]() ,价格保持第一批的价格不变;第三批购买男生保暖衣的价格在第一批购买的价格上每件减少了
,价格保持第一批的价格不变;第三批购买男生保暖衣的价格在第一批购买的价格上每件减少了![]() 元 ,女生保暖衣的价格比第一批购买的价格上每件增加了
元 ,女生保暖衣的价格比第一批购买的价格上每件增加了![]() 元,男生保暖衣的数量比第二批增加了
元,男生保暖衣的数量比第二批增加了![]() ,女生保暖衣的数量比第二批减少了
,女生保暖衣的数量比第二批减少了![]() ,第二批与第三批购买保暖衣的总费用相同,求
,第二批与第三批购买保暖衣的总费用相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根.

(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com