
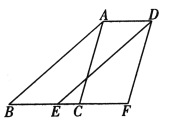
【题目】如图,B、E、C,F在一条直线上,AB∥DE,AC∥DF,BE=CF,连接AD.
求证:四边形ABED是平行四边形.
科目:初中数学 来源: 题型:
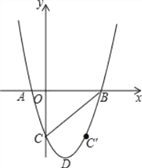
【题目】已知抛物线y=x2﹣4x﹣m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.
(1)若m=5时,求△ABD的面积.
(2)若在(1)的条件下,点E在线段BC下方的抛物线上运动,求△BCE面积的最大值.
(3)写出C点( , )、C′点( , )坐标(用含m的代数式表示)
如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,直接写出Q点和P点的坐标(可用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A.平行四边形,B.菱形,C.矩形,D.正方形,将这四张卡片背面朝上洗匀后.
(1)随机抽取一张卡片图案是轴对称图形的概率是 ;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是轴对称图形的概率,并用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.
![]()
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接五一节,重百超市计划销售枇杷和樱桃两种水果共5000千克,若枇杷的数量是樱桃的2倍少1000千克.
(1)超市计划销售枇杷多少千克?
(2)若超市从某一果园直接进货,果园共30名员工负责采摘这两种水果,每人每天能够采摘30千克枇杷或10千克樱桃,应分别安排多少人采摘枇杷和樱桃,才能确保采摘两种水果所用的时间相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
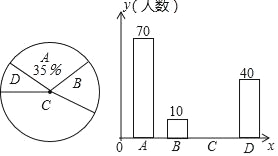
【题目】某校为提高学生课外阅读能力,决定向九年级学生推荐课外阅读书:A《热爱生命》; B:《平凡的世界》;C:《毛泽东传):;D:《牛虻》.并要求学生必须且只能选择一本阅读.为了解选择四种课外阅读书的学生人数,随机抽取了部分学生进行调查,并绘制以下两幅不完整的统计图.请根据统计图回答下列问题(要求写出简要的解答过程).
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校九年级总人数是1300人,请估计选择《毛泽东传》阅读的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
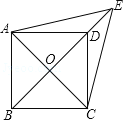
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第五个图形需要黑色棋子的个数是 ,第n个图形需要黑色棋子的个数是 (n≥1,且n为整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com