Question

【题目】如图，P是线段AB上一点，AB=12cm，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上），运动的时间为t.

（1）当t=1时，PD=2AC，请求出AP的长；

（2）当t=2时，PD=2AC，请求出AP的长；

（3）若C、D运动到任一时刻时，总有PD=2AC，请求出AP的长；

（4）在（3）的条件下，Q是直线AB上一点，且AQ﹣BQ=PQ，求PQ的长.

Answer 1

【答案】（1）4cm；（2）4cm；（3）4cm；（4）4cm或12cm

【解析】试题分析：

(1) 观察图形可以看出，图中的线段PC和线段BD的长分别代表动点C和D的运动路程. 利用“路程等于速度与时间之积”的关系可以得到线段PC和线段BD的长，进而发现BD=2PC. 结合条件PD=2AC，可以得到PB=2AP. 根据上述关系以及线段AB的长，可以求得线段AP的长.

(2) 利用“路程等于速度与时间之积”的关系结合题目中给出的运动时间，可以求得线段PC和线段BD的长，进而发现BD=2PC. 根据BD=2PC和PD=2AC的关系，依照第(1)小题的思路，可以求得线段AP的长.

(3) 利用“路程等于速度与时间之积”的关系可知，只要运动时间一致，点C与点D运动路程的关系与它们运动速度的关系一致. 根据题目中给出的运动速度的关系，可以得到BD=2PC. 这样，本小题的思路就与前两个小题的思路一致了. 于是，依照第(1)小题的思路，可以求得线段AP的长.

(4) 由于题目中没有指明点Q与线段AB的位置关系，所以应该按照点Q在线段AB上以及点Q在线段AB的延长线上两种情况分别进行求解. 首先，根据题意和相关的条件画出相应的示意图. 根据图中各线段之间的关系并结合条件AQ-BQ=PQ，得到AP和BQ之间的关系，借助前面几个小题的结论，即可求得线段PQ的长.

试题解析：

(1) 因为点C从P出发以1(cm/s)的速度运动，运动的时间为t=1(s)，所以 (cm).

因为点D从B出发以2(cm/s)的速度运动，运动的时间为t=1(s)，所以 (cm).

故BD=2PC.

因为PD=2AC，BD=2PC，所以BD+PD=2(PC+AC)，即PB=2AP.

故AB=AP+PB=3AP.

因为AB=12cm，所以 (cm).

(2) 因为点C从P出发以1(cm/s)的速度运动，运动的时间为t=2(s)，所以 (cm).

因为点D从B出发以2(cm/s)的速度运动，运动的时间为t=2(s)，所以 (cm).

故BD=2PC.

因为PD=2AC，BD=2PC，所以BD+PD=2(PC+AC)，即PB=2AP.

故AB=AP+PB=3AP.

因为AB=12cm，所以 (cm).

(3) 因为点C从P出发以1(cm/s)的速度运动，运动的时间为t(s)，所以 (cm).

因为点D从B出发以2(cm/s)的速度运动，运动的时间为t(s)，所以 (cm).

故BD=2PC.

因为PD=2AC，BD=2PC，所以BD+PD=2(PC+AC)，即PB=2AP.

故AB=AP+PB=3AP.

因为AB=12cm，所以 (cm).

(4) 本题需要对以下两种情况分别进行讨论.

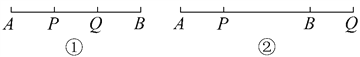
(1) 点Q在线段AB上(如图①).

因为AQ-BQ=PQ，所以AQ=PQ+BQ.

因为AQ=AP+PQ，所以AP=BQ.

因为，所以.

故.

因为AB=12cm，所以 (cm).

(2) 点Q不在线段AB上，则点Q在线段AB的延长线上(如图②).

因为AQ-BQ=PQ，所以AQ=PQ+BQ.

因为AQ=AP+PQ，所以AP=BQ.

因为，所以.

故.

因为AB=12cm，所以 (cm).

综上所述，PQ的长为4cm或12cm.