

 ×DE-
×DE- AE×EC-
AE×EC- BD×DC,
BD×DC, ×(a+b)-
×(a+b)- ab-
ab- ab,
ab, (a2+b2),
(a2+b2),
 ×DE,
×DE, ×(b-a),
×(b-a),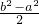 .
.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
 25、画图并讨论:
25、画图并讨论:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:河北省2012年中考数学试题 题型:044
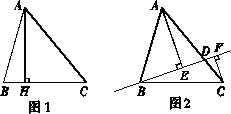
如图1和图2,在△ABC中,AB=13,BC=14,cos∠ABC=![]() .
.
探究
在如图1,AH⊥BC于点H,则AH=________,AC=________,△ABC的面积S△ABC=________.
拓展
如图2,点D在AC上(可与点A,B重合),分别过点A,C作直线BD的垂线,垂足为E,F.设BD=x,AE=m,CF=n.(当点D与点A重合时,我们认为S△ABC=0.
(1)用含x,m或n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值.
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现
请你确定一条直线,使得A,B,C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市2011年初中毕业生升学文化课考试数学试卷 题型:059
如图(1)至图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,点B、C、E在同一条直线上.

(1)已知:如图(1),AC=AB,AD=AE.求证:①CD=BE;②CD⊥BE.
(2)如图(2),当AB=kAC,AE=kAD(k≠1)时,分别说出(1)中的两个结论是否成立,若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com