
【题目】方程也可以用来解决一些几何问题,如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,设△BPD的面积为![]() ,△CPE的面积为
,△CPE的面积为![]() ,
,
(1)![]()
![]() ;
;![]()
![]() (填数字);
(填数字);
(2)求![]() 的值.
的值.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动.星期天的上午小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°. 为了便于观察.小明迅速向前边移动边收线到达了离A处7米的B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在冋一条直线上,∠ACD=90°.请你求出小明此吋所收回的风筝线的长度是多少米?(本题中风筝线均视为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732.最后结果精确到1米)
≈1.732.最后结果精确到1米)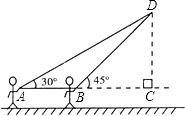
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如下表所示:

某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲、乙两班分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点(小正方形的顶点叫格点)上,连接BD.

(1)利用格点在图中画出△ABD中AD边上的高,垂足为H.
(2)①画出将△ABD先向右平移2格,再向上平移2格得到的△A1B1D1;
②平移后,求线段AB扫过的部分所组成的封闭图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
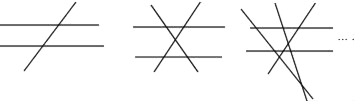
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com