
【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(﹣2,1).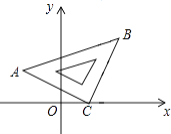
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
【答案】
(1)解:过点A作AD⊥x轴,垂足为D.
∵C(1,0),A(﹣2,1),
∴AD=1,DC=1﹣(﹣2)=3,
∴AC2=AD2+DC2=10,
∴S△ABC= ![]() AC2=5
AC2=5
(2)解:过点B作BE⊥x轴,垂足为E, 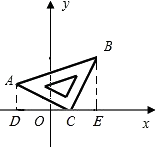
∴∠ADC=∠CEB=90°,
∴∠CAD+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ADC和△CEB中,
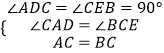 ,
,
∴△ADC≌△CEB,
∴CD=BE=3,CE=AD=1,
∴OE=2,
∴点B的坐标为(2,3).
设直线AB的解析式为y=kx+b,则
![]() ,
,
解得 ![]() ,
,
∴y= ![]() x+2.
x+2.
当x=0时,y=2,
∴直线AB交y轴于点(0,2).
【解析】(1)过点A作AD⊥x轴,垂足为D,由C,D两点的坐标得出AD,DC的长然后用勾股定理得出AC的长,利用直角三角形的面积计算方法得出答案;
(2)过点B作BE⊥x轴,垂足为E,根据直角三角形两锐角互余,及同角的余角相等得出∠CAD=∠BCE,然后由AAS得出△ADC≌△CEB,根据全等三角形的性质得出CD=BE=3,CE=AD=1,故OE=2,从而得出B点的坐标,用待定系数法求出直线AB的解析式,进而求出直线AB与y轴交点的坐标。
【考点精析】关于本题考查的确定一次函数的表达式和勾股定理的概念,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,以A(0, ![]() )为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
)为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
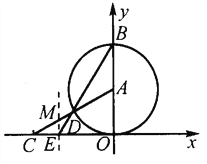
(1)分别求点E、C的坐标;
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式;
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心,ME为半径的圆与⊙A的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示( )
A.支出20元
B.收入20元
C.支出80元
D.收入80元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为![]()
(1)试求袋中绿球的个数;

(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com