
【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式.
(2)若α为锐角,tanα= ![]() ,当AE取得最小值时,求正方形OEFG的面积.
,当AE取得最小值时,求正方形OEFG的面积.
(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为 ![]() :1?若能,求点P的坐标;若不能,试说明理由
:1?若能,求点P的坐标;若不能,试说明理由
【答案】
(1)
解:如图1,
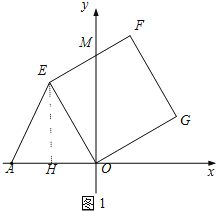
过点E作EH⊥OA于点H,EF与y轴的交点为M.
∵OE=OA,α=60°,
∴△AEO为正三角形,
∴OH=3,EH= ![]() =3
=3 ![]() .
.
∴E(﹣3,3 ![]() ).
).
∵∠AOM=90°,
∴∠EOM=30°.
在Rt△EOM中,
∵cos∠EOM= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴OM=4 ![]() .
.
∴M(0,4 ![]() ).
).
设直线EF的函数表达式为y=kx+4 ![]() ,
,
∵该直线过点E(﹣3,3 ![]() ),
),
∴﹣3k+4 ![]() =3
=3 ![]() ,
,
解得k= ![]() ,
,
所以,直线EF的函数表达式为y= ![]() x+4
x+4 ![]()
(2)
解:如图2,
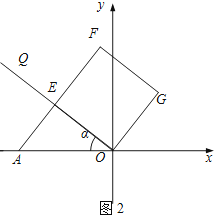
射线OQ与OA的夹角为α( α为锐角,tanα ![]() ).
).
无论正方形边长为多少,绕点O旋转角α后得到正方
形OEFG的顶点E在射线OQ上,
∴当AE⊥OQ时,线段AE的长最小.
在Rt△AOE中,设AE=a,则OE=2a,
∴a2+(2a)2=62,解得a1= ![]() ,a2=﹣
,a2=﹣ ![]() (舍去),
(舍去),
∴OE=2a= ![]()
,∴S正方形OEFG=OE2= ![]()
(3)
解:设正方形边长为m.
当点F落在y轴正半轴时.
如图3,
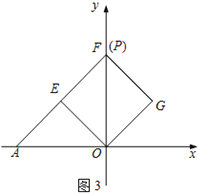
当P与F重合时,△PEO是等腰直角三角形,有 ![]() =
= ![]() 或
或 ![]() =
= ![]() .
.
在Rt△AOP中,∠APO=45°,OP=OA=6,
∴点P1的坐标为(0,6).
在图3的基础上,
当减小正方形边长时,
点P在边FG 上,△OEP的其中两边之比不可能为 ![]() :1;
:1;
当增加正方形边长时,存在 ![]() =
= ![]() (图4)和
(图4)和 ![]() =
= ![]() (图5)两种情况.
(图5)两种情况.
如图4,
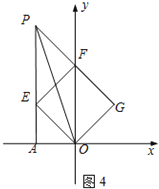
△EFP是等腰直角三角形,
有 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
此时有AP∥OF.
在Rt△AOE中,∠AOE=45°,
∴OE= ![]() OA=6
OA=6 ![]() ,
,
∴PE= ![]() OE=12,PA=PE+AE=18,
OE=12,PA=PE+AE=18,
∴点P2的坐标为(﹣6,18).
如图5,
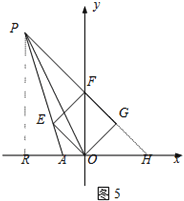
过P作PR⊥x轴于点R,延长PG交x轴于点H.设PF=n.
在Rt△POG中,PO2=PG2+OG2=m2+(m+n)2=2m2+2mn+n2,
在Rt△PEF中,PE2=PF2+EF2=m2+n2,
当 ![]() =
= ![]() 时,
时,
∴PO2=2PE2.
∴2m2+2mn+n2=2(m2+n2),得n=2m.
∵EO∥PH,
∴△AOE∽△AHP,
∴ ![]() =
= ![]() ,
,
∴AH=4OA=24,
即OH=18,
∴m=9 ![]() .
.
在等腰Rt△PRH中,PR=HR= ![]() PH=36,
PH=36,
∴OR=RH﹣OH=18,
∴点P3的坐标为(﹣18,36).
当点F落在y轴负半轴时,
如图6,
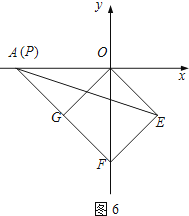
P与A重合时,在Rt△POG中,OP= ![]() OG,
OG,
又∵正方形OGFE中,OG=OE,
∴OP= ![]() OE.
OE.
∴点P4的坐标为(﹣6,0).
在图6的基础上,当正方形边长减小时,△OEP的其中
两边之比不可能为 ![]() :1;当正方形边长增加时,存在
:1;当正方形边长增加时,存在 ![]() =
= ![]() (图7)这一种情况.
(图7)这一种情况.
如图7,过P作PR⊥x轴于点R,
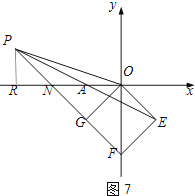
设PG=n.
在Rt△OPG中,PO2=PG2+OG2=n2+m2,
在Rt△PEF中,PE2=PF2+FE2=(m+n )2+m2=2m2+2mn+n2.
当 ![]() =
= ![]() 时,
时,
∴PE2=2PO2.
∴2m2+2mn+n2=2n2+2m2,
∴n=2m,
由于NG=OG=m,则PN=NG=m,
∵OE∥PN,∴△AOE∽△ANP,∴ ![]() =1,
=1,
即AN=OA=6.
在等腰Rt△ONG中,ON= ![]() m,
m,
∴12= ![]() m,
m,
∴m=6 ![]() ,
,
在等腰Rt△PRN中,RN=PR=6,
∴点P5的坐标为(﹣18,6).
所以,△OEP的其中两边的比能为 ![]() :1,点P的坐标是:P1(0,6),P2(﹣6,18),
:1,点P的坐标是:P1(0,6),P2(﹣6,18),
P3(﹣18,36),P4(﹣6,0),P5(﹣18,6)
【解析】(1)先判断出△AEO为正三角形,再根据锐角三角函数求出OM即可;(2)判断出当AE⊥OQ时,线段AE的长最小,用勾股定理计算即可;(3)由△OEP的其中两边之比为 ![]() :1分三种情况进行计算即可.此题是正方形的性质题,主要考查了正方形的性质,等腰三角形的性质,勾股定理,解本题的关键是灵活运用勾股定理进行计算.
:1分三种情况进行计算即可.此题是正方形的性质题,主要考查了正方形的性质,等腰三角形的性质,勾股定理,解本题的关键是灵活运用勾股定理进行计算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为正整数),则有a+b
)2(其中a、b、m、n均为正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,
,
∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得:a= , b= .
)2,用含m、n的式子分别表示a、b,得:a= , b= .
(2)利用所探索的结论,找一组正整数a、b、m、n填空: + = ( + )2;(答案不唯一)
(3)若a+4![]() =(m+n
=(m+n![]() )2 ,且a、m、n均为正整数,求a的值.
)2 ,且a、m、n均为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;

(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
①面积相等的两个直角三角形全等;
②对角线互相垂直的四边形是正方形;
③将抛物线 ![]() 向左平移4个单位,再向上平移1个单位可得到抛物线
向左平移4个单位,再向上平移1个单位可得到抛物线 ![]() ;
;
④两圆的半径R、r分别是方程x2-3x+2=0 的两根,且圆心距d=3, 则两圆外切.
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )

A. 正方形 B. 菱形 C. 矩形 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知:如图1,直线AB∥CD,点E是AB、CD之间的一点,连接BE、DE得到∠BED.
求证:∠BED =∠B+∠D.
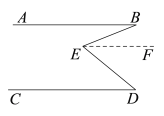 图1
图1
小冰是这样做的:
证明:过点E作EF∥AB,则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF +∠FED =∠B+∠D.
即∠BED=∠B+∠D.
请利用材料中的结论,完成下面的问题:
已知:直线 AB∥CD,直线MN分别与AB、CD交于点E、F.
(1)如图2,∠BEF和∠EFD的平分线交于点G.猜想∠G的度数,并证明你的猜想;
(2)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2.求证:∠FG1 E+∠G2=180°.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com