练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知a、b、c为实数，且多项式x3+ax2+bx+c能被x2+3x-4整除，则2a-2b-c=________．

    14
    分析：由于x2+3x-4=（x+4）（x-1），而多项式x3+ax2+bx+c能被x2+3x-4整除，则x3+ax2+bx+c能被（x+4）（x-1）整除，即-4，1是方程x3+ax2+bx+c=0的两根，把x=-4和x=1分别代入x3+ax2+bx+c=0，得到关于a、b、c的三元一次方程组，将此方程组变形，即可得到2a-2b-c的值．
    解答：∵x2+3x-4=（x+4）（x-1），
    ∴x3+ax2+bx+c能被（x+4）（x-1）整除，
    即-4，1是方程x3+ax2+bx+c=0的两根．
    把x=-4和x=1分别代入x3+ax2+bx+c=0，得，
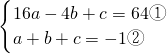
    ①-②×6，得10a-10b-5c=70，
    两边除以5，得2a-2b-c=14．
    故答案为14．
    点评：本题主要考查了整式乘除法与因式分解的关系及求代数式的值的方法，属于竞赛题型，有一定难度．本题的关键是能够通过整式乘除法与因式分解的关系得出x3+ax2+bx+c含有因式（x+4）（x-1），从而可知-4，1是方程x3+ax2+bx+c=0的两根．难点是列出方程组之后将其变形，从而求出2a-2b-c的值．
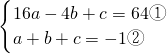    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知a，b，c为实数，且满足下式：a2+b2+c2=1，①，a(
    1
    b
    +
    1
    c
    )+b(
    1
    c
    +
    1
    a
    )+c(
    1
    a
    +
    1
    b
    )=-3    ；②求a+b+c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a、b、c为实数，设A=a2-2b+
    π
    3
    ，B=b2-2c+
    π
    3
    ，C=c2-2a+
    π
    3
    ．
    （1）判断A+B+C的符号并说明理由；
    （2）证明：A、B、C中至少有一个值大于零．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a、b、c为实数，且
    ab
    a+b
    =
    1
    3
    ，
    bc
    b+c
    =
    1
    4
    ，
    ca
    c+a
    =
    1
    5
    ．求
    abc
    ab+bc+ca
    的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    14、已知a，b，c为实数，下列命题中，假命题是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a，b，c为实数，且多项式x3+ax2+bx+c能够被x2+3x-4整除．
    （1）求4a+c的值；
    （2）求2a-2b-c的值．

    查看答案和解析>>

    同步练习册答案