
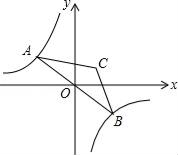
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
科目:初中数学 来源: 题型:
【题目】2019年9月,在郑州举行的第十一届全国少数民族运动会的龙舟比赛中,甲、乙两队在![]() 米的赛道上,所划行的路程
米的赛道上,所划行的路程![]() 与时间
与时间![]() 之间的函数关系式如图所示,下列说法错误的是( )
之间的函数关系式如图所示,下列说法错误的是( )
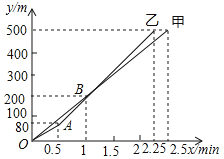
A.乙队比甲队提前![]() 到达终点
到达终点
B.当乙队划行![]() 时,此时落后甲队
时,此时落后甲队![]()
C.![]() 后,乙队比甲队每分钟快
后,乙队比甲队每分钟快![]()
D.自![]() 开始,甲队若要与乙队同时到达终点,甲队的速度需提高到
开始,甲队若要与乙队同时到达终点,甲队的速度需提高到![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
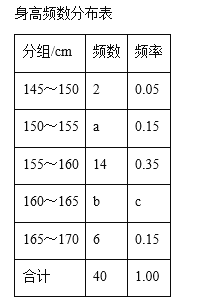
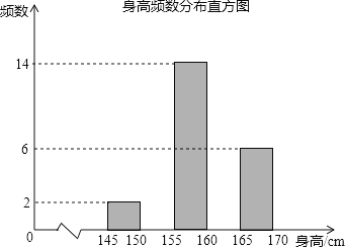
【题目】为了了解初中阶段女生身高情况,从某中学初二年级120名女生中随意抽出40名同龄女生的身高数据,经过分组整理后的频数分布表及频数分布直方图如图所示:
结合以上信息,回答问题:
(1)a=______,b=______,c=______.
(2)请你补全频数分布直方图.
(3)试估计该年级女同学中身高在160~165cm的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
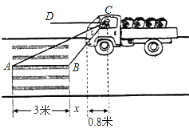
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
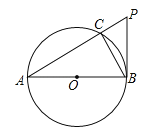
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com