
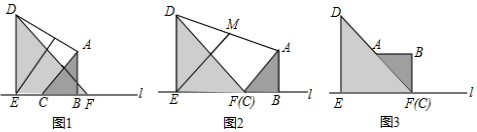
分析 (1)根据题意可得EM垂直平分DF,直线AF∥EM,从而$\frac{DM}{AM}$转化为$\frac{DO}{OF}$,继而得出结论;
(2)仿照(1)的思路进行求解即可;
(3)先补全图形,连接AE,分别求出AM及DM的值,然后可确定比值.
解答 解:(1)如图1,
∵∠MEB=45°,∠AFB=45°,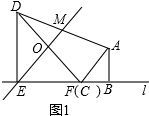
∴EM垂直且平分DF,AF∥EM,
∴$\frac{DM}{AM}$=$\frac{DO}{OF}$=1;
(2)如图2,由(1)可得 $\frac{DM}{AM}$=$\frac{DO}{OH}$=$\frac{OF}{OH}$=$\frac{EF}{EC}$,
∵EF=DE=2,CE=x
∴$\frac{DM}{AM}$=$\frac{2}{x}$,
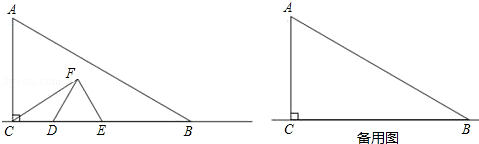
(3)连接AE,补全图形如图3所示,
∵△ABC,△DEF均为等腰直角三角形,DE=2,AB=1,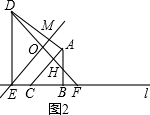
∴EF=2,BC=1,∠DEF=90°,∠4=∠5=45°
∴DF=2$\sqrt{2}$,AC=$\sqrt{2}$,∠EFB=90°
∴DF=2AC,AD=$\sqrt{2}$,
∴点A为CD的中点,
∴EA⊥DF,EA平分∠DEF,
∴∠MAE=90°,∠AEF=45°,AE=$\sqrt{2}$,
∵∠BEM=45°,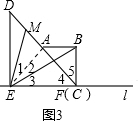
∴∠1+∠2=∠3+∠2=45°,
∴∠1=∠3,FFF
∴△AEM∽△FEB,
∴$\frac{AM}{BF}=\frac{AE}{EF}$,
∴AM=$\frac{\sqrt{2}}{2}$,
∴DM=AD-AM=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{DM}{AM}$=1.
点评 本题考查了相似形综合题,涉及了相似三角形的判定与性质、平行线的性质、旋转的性质及等腰直角三角形的性质,考察的知识点比较多,难度较大,解答本题之前一定要将图形画出来,这样可以使我们的思考方向更准确一些,另外要求我们熟练掌握各个基础知识点的内容.


科目:初中数学 来源: 题型:解答题
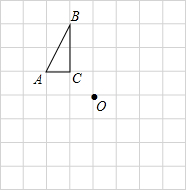 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com