

分析 (1)根据时间和速度表示出OE、OF,根据锐角三角函数的概念列式计算即可;
(2)作EH⊥AB于H,证明△FOM∽△EHA,得到∠FMO=∠EAH,得到答案;
(3)作NP∥OA交OB于P,根据平行线分线段成比例定理,求出NP的长,列出比例式求解即可.
解答 解(1)∵正方形边长为6$\sqrt{2}$,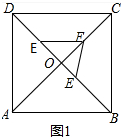
∴AC=BD=12,OA=OB=6,
当点E在OB上时,
∠FEO=60°,
tan∠FEO=$\frac{OF}{OE}$,
即$\frac{t}{6-2t}$=$\sqrt{3}$,
解得,t=$\frac{36-6\sqrt{3}}{11}$,
当点E在OD上时,
同理可得,t=$\frac{36+6\sqrt{3}}{11}$.
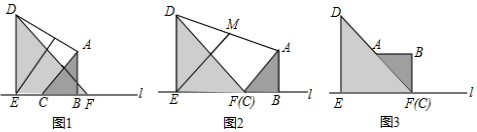
(2)如图2,作EH⊥AB于H,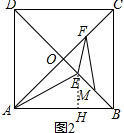
由题意得,OF=t,OM=6-t,$\frac{OF}{OM}$=$\frac{t}{6-t}$,
∵BE=2t,∠EBH=45°,
∴EH=BH=$\sqrt{2}$t,AH=6$\sqrt{2}$-$\sqrt{2}$t,
$\frac{EH}{AH}$=$\frac{\sqrt{2}t}{6\sqrt{2}-\sqrt{2}t}$=$\frac{t}{6-t}$,
$\frac{OF}{OM}$=$\frac{EH}{AH}$,∠FOM=∠EHA=90°,
∴△FOM∽△EHA,
∴∠FMO=∠EAH,
∴∠OAE+∠OMF=∠OAE+∠EAH=45°.
(3)如图3,F、E、N三点在同一条直线上时,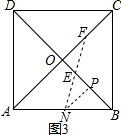
作NP∥OA交OB于P,
∵N为AB的中点,
∴NP=$\frac{1}{2}$OA=3,
∴$\frac{NP}{OF}$=$\frac{PE}{EO}$,
即$\frac{3}{t}$=$\frac{2t-3}{6-2t}$,
解得,t=$\frac{-3±\sqrt{153}}{4}$,
根据题意,t=$\frac{-3+\sqrt{153}}{4}$.
点评 本题考查的是正方形的性质,根据点移动的时间和速度表示出线段的长度、结合相似三角形的性质列出方程是解题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
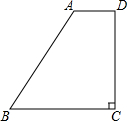 如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
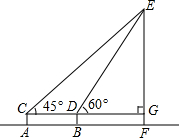 如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为(10.6+3$\sqrt{3}$)米.(结果用带根号的式子表示)
如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为(10.6+3$\sqrt{3}$)米.(结果用带根号的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
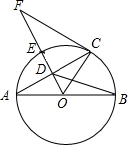 如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2.
如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com