单项式-$\frac{1}{2}$a2x-1b2是5次单项式.则x=2．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

12．单项式-$\frac{1}{2}$a^2x-1b²是5次单项式，则x=2．

分析根据单项式的次数是得出2x-1+2=5，得出x的值即可．

解答解：∵单项式-$\frac{1}{2}$a^2x-1b²是5次单项式，
∴2x-1+2=5，
解得x=2，
故答案为2．

点评本题考查了单项式，掌握单项式的次数和系数是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

2．

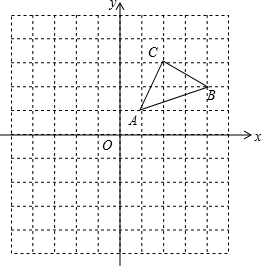如图，方格纸中的每个小方格都是边长为1个单位的小正方形，每个小正方形的顶点称为格点．△ABC的顶点都在格点上，建立平面直角坐标系后，点A、B、C的坐标分别为（1，1），（4，2），（2，3）．（提示：一定要用铅笔作图）
（1）画出△ABC向左平移4个单位，再向上平移1个单位后得到的△A₁B₁C₁；
（2）画出△ABC向关于x轴对称的△A₂B₂C₂；
（3）以点A、A₁、A₂为顶点的三角形的面积为4．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

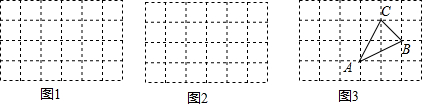如图网格图中，每个小正方形的边长均为1，每个小格的顶点叫做格点．
（1）请在图1中，画一个格点三角形，使它的三边长都是有理数；
（2）请在图2中，画一个格点三角形，使它的三边长都是无理数；
（3）图3中的△ABC的面积为$\frac{3}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．计算：（-4）²÷4²+3×（-6）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．阅读理解：
如图1，若在四边形ABCD的边AB上任取一点E（点E与点A，B不重合），分别连结ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：
（1）如图1，若∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由．
（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，在图2中作出矩形ABCD的边AB上的一个强相似点E．（作出一个即可，不限作图工具）
拓展探究：
（3）如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，则S_△AME：S_△MEC=1：3（直接写出结果）．

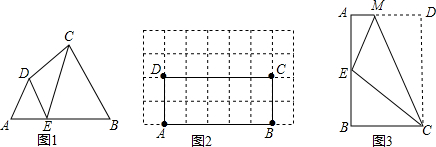
查看答案和解析>>

科目：初中数学 来源： 题型：选择题

17．

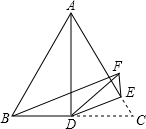如图，△ABC是等边三角形，AD是BC边上的中线，点E在AC上，∠CDE=25°，现将
△CDE沿直线DE翻折得到△FDE，连接BF，则∠BFE的度数是（　　）

A．

60°

B．

68°

C．

75°

D．

85°

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．

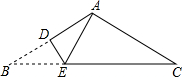如图，△ABC是一张顶角为120°的三角形纸片，AB=AC，BC=6，现将△ABC折叠，使点B与点A 重合，折痕为DE，则DE的长为（　　）

A．

B．

C．

$2\sqrt{3}$

D．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．

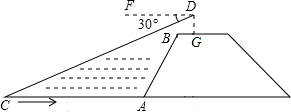如图，小黄站在河岸上的G点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船C的俯角是∠FDC=30°，若小黄的眼睛与地面的距离DG是1.6米，BG=0.7米，BG平行于AC所在的直线，迎水坡AB的坡度为i=4：3，坡长AB=10.5米，则此时小船C到岸边的距离CA的长为（　　）米．（$\sqrt{3}$≈1.7，结果保留两位有效数字）

A．

B．

8.5

C．

7.2

D．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．下列说法正确的是（　　）

	A．	0是最小的整数
	B．	若\|a\|=\|b\|，则a=b
	C．	互为相反数的两数之和为零
	D．	数轴上两个有理数，较大的数离原点较远

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学