

分析 (1)连接BD,证明BD为⊙O的直径,由FD为⊙O的切线,则∠BDE=90°,所以△BDE是等腰直角三角形,所以∠E=45°;
(2)设∠QAB=α,∠GBE=β,则α+β=45°,根据三角函数得:tan∠α=$\frac{DG}{BD}=\frac{BQ}{AB}$,因为△ABD是等腰直角三角形,则BD=$\sqrt{2}$AB,代入比例式可得结论;
(3)如图3,连接AH,证明△APB≌△AHD(AAS),则DH=PB,设DH=x,则PH=PB+PH=6+x,GH=1,由三角函数列式得:tan∠α=$\frac{HG}{HD}$=$\frac{DH}{BH}$,代入可得x的值,利用勾股定理计算BD的长,BD为⊙O的直径,所以可得半径的长.
解答 解:(1)如图1,连接BD,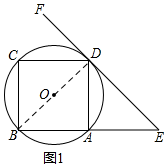
∵四边形ABCD是正方形,
∴∠BAD=90°,∠DBA=45°,
∴BD为⊙O的直径,
∵FD为⊙O的切线,
∴BD⊥FD,
∴∠BDE=90°,
∴∠E=45°;
(2)如图2,设∠QAB=α,∠GBE=β,则α+β=45°,
∵∠DBE=45°,
∴∠DBG=∠QAB=α,
Rt△BDG中,tan∠α=$\frac{DG}{BD}$,
Rt△ABQ中,tan∠α=$\frac{BQ}{AB}$,
∴$\frac{DG}{BD}=\frac{BQ}{AB}$,
∵Rt△ABD中,cos∠ABD=cos45=$\frac{AB}{BD}$=$\frac{\sqrt{2}}{2}$,
∴BD=$\sqrt{2}$AB,
∴$\frac{DG}{\sqrt{2}AB}=\frac{BQ}{AB}$,
∴DG=$\sqrt{2}$BQ;
(3)连接AH,
∵∠BHA=∠ADB=45°,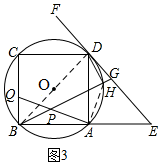
∴∠APH=∠BHA=45°,
∴∠PAH=90°,
∵∠BAD=90°,
∴∠BAP=∠DAH,
∵BD为⊙O的直径,
∴∠DHB=90°,
∴∠DHA=90°+45°=135°,
∵∠BPA=180°-45°=135°,
∴∠BPA=∠DHA,
在△APB和△AHD中,
∵$\left\{\begin{array}{l}{AB=AD}\\{∠BAP=∠DAH}\\{∠APB=∠AHD}\end{array}\right.$,
∴△APB≌△AHD(AAS),
∴DH=PB,
设DH=x,则PH=PB+PH=6+x,GH=1,
∵∠BDG=90°,
∴∠HDG=∠DBG=∠α,
Rt△DHG中,tan∠α=$\frac{HG}{HD}$,
Rt△BDH中,tan∠α=$\frac{DH}{BH}$,
∴$\frac{HG}{HD}=\frac{DH}{BH}$,
∴DH2=HG•BH,
∴x2=1×(6+x),
x2-x-6=0,
(x-3)(x+2)=0,
x1=3,x2=-2(舍),
∴DH=3,BH=9,
∴BD=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$,
∴⊙O的半径为$\frac{3\sqrt{10}}{2}$.
点评 本题考查了正方形的性质、三角形全等的性质和判定、三角函数、切线的性质以及圆内接四边形的性质等知识,第二问有难度,利用等角的三角函数列式或证明△BDG∽△ABQ可得结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
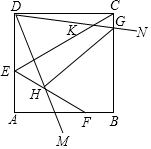 正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.
正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
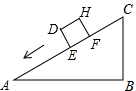 一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.| A. | $\frac{16}{3}$ | B. | $\frac{14}{3}$ | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
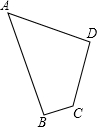 如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的统计图,下面有四个推断:
“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的统计图,下面有四个推断:| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com