Question

如图，已知菱形AOBD的A、B、D三点在⊙O上，延长BO至点P，交⊙O于点C，且BP=3OB．

求证：AP是⊙O的切线．

 

 

Answer 1

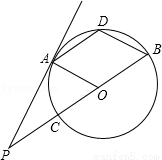
证明见解析.

【解析】

试题分析：连接OD、AO，根据菱形的性质得AO=OB=BD=DA，则可判断△OAD和△OBD都为等边三角形，所以∠AOD=∠BOD=60°，则∠AOP=60°，于是又可判断△AOC为等边三角形，所以AC=OC，∠ACO=∠OAC=60°，由PB=3BO得到CP=OC=AC，根据等腰三角形的性质得∠P=∠CAP，然后利用三角形外角性质有∠P+∠CAP=∠ACO=60°，得到∠CAP=30°，所以∠OAP=90°，最后利用切线的判定定理得到AP为⊙O的切线．

试题解析：证明：连接OD、AO，如图，

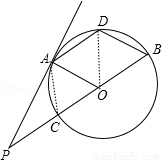
∵四边形AOBD为菱形，

∴AO=OB=BD=DA，

∴△OAD和△OBD都为等边三角形，

∴∠AOD=∠BOD=60°，

∴∠AOP=60°，

又∵OA=OC，

∴△AOC为等边三角形，

∴AC=OC，∠ACO=∠OAC=60°，

∵PB=3BO，OC=OB，

∴CP=OC=AC，

∴∠P=∠CAP，

∵∠P+∠CAP=∠ACO=60°，

∴∠CAP=30°，

∴∠OAP=90°，

∴OA⊥AP，

∴AP为⊙O的切线．

考点：切线的判定．